Prova Matemática Enem 2016 comentada
Veja aqui a correção da prova de Matemática do segundo dia. Prova Matemática Enem 2016 comentada !
QUESTÃO 136 – Enem 2016 prova azul
Em regiões agrícolas, é comum a presença de silos para armazenamento e secagem da produção de grãos, no formato de um cilindro reto, sobreposto por um cone, e dimensões indicadas na figura. O silo fica cheio e o transporte dos grãos é feito em caminhões de carga cuja capacidade é de 20 m3. Uma região possui um silo cheio e apenas um caminhão para transportar os grãos para a usina de beneficiamento.
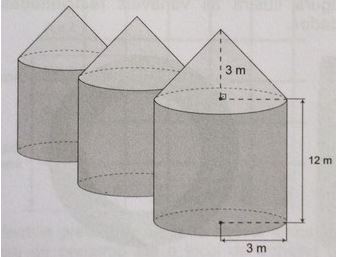 Utilize 3 como aproximação para π.
O número mínimo de viagens que o caminhão precisará fazer para transportar todo o volume de grãos armazenados no Silo é
a) 6.
b) 16.
c) 17.
d) 18.
e) 21.
Resolução Questão 136 – Prova Azul
Utilize 3 como aproximação para π.
O número mínimo de viagens que o caminhão precisará fazer para transportar todo o volume de grãos armazenados no Silo é
a) 6.
b) 16.
c) 17.
d) 18.
e) 21.
Resolução Questão 136 – Prova Azul
Vsilo = Vcilindro + Vcone
Vsilo = Ab.h +Ab.h/3 =
Vsilo = π.Rci2.h + π.Rco2.h/3
Vsilo = π.32.12 + π.32.3/3 =
Vsilo = 117 π =
Vsilo = 117.3 = 351
Número de viagens = 351/20 = 17,55 ≈18
Resposta D
Prova Matemática Enem 2016 comentada
QUESTÃO 137 – Enem 2016 prova azul
Em uma empresa de móveis, um cliente encomenda um guarda-roupa nas dimensões 220 cm de altura, 120 cm de largura e 50 cm de profundidade. Alguns dias depois, o projetista, com o desenho elaborado na escala 1 : 8, entra em contato com o cliente para fazer sua apresentação. No momento da impressão, o profissional percebe que o desenho não caberia na folha de papel que costumava usar. Para resolver o problema, configurou a impressora para que a figura fosse reduzida em 20%.
A altura, a largura e a profundidade do desenho impresso para a apresentação serão, respectivamente,
a) 22,00 cm, 12,00 cm e 5,00 cm.
b) 27,50 cm, 15,00 cm e 6,25 cm.
c) 34,37 cm, 18,75 cm e 7,81 cm.
d) 35,20 cm, 19,20 cm e 8,00 cm.
e) 44,00 cm, 24,00 cm e 10.00 cm.
Resolução Questão 137 – Prova Azul
Inicialmente, ao elaborar o desenho na escala 1 : 8, dividem-se todas as medidas por 8. Em seguida, reduz-se a figura em 20%, o que é equivalente a multiplicar as medidas por 0,8. Assim, as medidas finais do desenho são:
Real:
Altura = h = 220cm
Largura = L = 120cm
Profundidade = P = 50cm
Escala 1:8
Desenho:
h = 220cm/8 = 27,5
L = 120/8 = 15
P = 50/8=6,25
Redução 20%:
h = 27,5 . 0,8 = 22 cm
L = 15 . 0,8 = 12 cm
P = 6,25 . 0,8 = 5 cm
Resposta A
Prova Matemática Enem 2016 comentada
QUESTÃO 138 – Enem 2016 prova azul
A London Eye é uma enorme roda-gigante na capital inglesa. Por ser um dos monumentos construídos para celebrar a entrada do terceiro milênio, ela também é conhecida como Roda do Milênio. Um turista brasileiro, em visita à Inglaterra, perguntou a um londrino o diâmetro (destacado na imagem) da Roda do Milênio e ele respondeu que ele tem 443 pés.
 Disponível em: www.mapadelondres.org. Acesso em 14 maio 2015 (adaptado).
Não habituado com a unidade pé, e querendo satisfazer sua curiosidade, esse turista consultou um manual de unidades de medidas e constatou que 1 pé equivale a 12 polegadas, e que 1 polegada equivale a 2,54 cm. Após alguns cálculos de conversão, o turista ficou surpreendido com o resultado obtido em metros.
Qual a medida que mais se aproxima do diâmetro da Roda do Milênio, em metro?
a) 53
b) 94
c) 113
d) 135
e) 145
Resolução Questão 138 – Prova Azul
Diâmetro = 443 pés
Diâmetro = 443 . 12 = 5316 polegadas
Diâmetro = 5316 . 2,54cm
Diâmetro ≈ 13502 cm
Diâmetro ≈ 135,02 m
Resposta D
Disponível em: www.mapadelondres.org. Acesso em 14 maio 2015 (adaptado).
Não habituado com a unidade pé, e querendo satisfazer sua curiosidade, esse turista consultou um manual de unidades de medidas e constatou que 1 pé equivale a 12 polegadas, e que 1 polegada equivale a 2,54 cm. Após alguns cálculos de conversão, o turista ficou surpreendido com o resultado obtido em metros.
Qual a medida que mais se aproxima do diâmetro da Roda do Milênio, em metro?
a) 53
b) 94
c) 113
d) 135
e) 145
Resolução Questão 138 – Prova Azul
Diâmetro = 443 pés
Diâmetro = 443 . 12 = 5316 polegadas
Diâmetro = 5316 . 2,54cm
Diâmetro ≈ 13502 cm
Diâmetro ≈ 135,02 m
Resposta D
Prova Matemática Enem 2016 comentada
QUESTÃO 139- Enem 2016 prova azul
Uma cisterna de 6 000 L foi esvaziada em um período de 3 h. Na primeira hora foi utilizada apenas uma bomba, mas nas duas horas seguintes, a fim de reduzir o tempo de esvaziamento, outra bomba foi ligada junto com a primeira. O gráfico, formado por dois segmentos de reta, mostra o volume de água presente na cisterna, em função do tempo.

Qual é a vazão, em litro por hora, da bomba que foi ligada no início da segunda hora?
a) 1 000
b) 1 250
c) 1 500
d) 2 000
e) 2 500
Resolução
Do gráfico, sendo V1 a vazão da bomba ligada primeiro e V2 a da aberta ao fim da primeira hora, tem-se:
Bomba 1
Vazão = ∆y/ ∆x
Vazão = 1000/1 = 1000
Bomba 1 e 2
Vazão = ∆y/ ∆x
Vazão = 5000/2 = 2500
Logo a vazão da bomba 2 é:
2500 – 1000 = 1500 L/h
Resposta C
Prova Matemática Enem 2016 comentada
QUESTÃO 140- Enem 2016 prova azul
O procedimento de perda rápida de “peso” é comum entre os atletas dos esportes de combate. Para participar de um torneio, quatro atletas da categoria até 66 kg, Peso-Pena, foram submetidos a dietas balanceadas e atividades físicas. Realizaram três “pesagens” antes do início do torneio. Pelo regulamento do torneio, a primeira luta deverá ocorrer entre o atleta mais regular e o menos regular quanto aos “pesos”. As informações com base nas pesagens dos atletas estão no quadro.
 Após as três “pesagens”, os organizadores do torneio informaram aos atletas quais deles se enfrentariam na primeira luta.
A primeira luta foi entre os atletas
a) I e III.
b) I e IV.
c) II e III.
d) II e IV.
e) III e IV.
Resolução
Em casos de empate, o atleta de melhor desempenho e mais regular é aquele que não se afasta da média ou seja o de menor desvio padrão.
Nesse caso foi o Atleta III é o mais regular (menor desvio padrão)
o Atleta II é o menos regular (maior desvio padrão).
Na terceira pesagem todos bateram o peso de 66kg e portanto aptos para lutar.
Então a primeira luta será entre os atletas II e III
Após as três “pesagens”, os organizadores do torneio informaram aos atletas quais deles se enfrentariam na primeira luta.
A primeira luta foi entre os atletas
a) I e III.
b) I e IV.
c) II e III.
d) II e IV.
e) III e IV.
Resolução
Em casos de empate, o atleta de melhor desempenho e mais regular é aquele que não se afasta da média ou seja o de menor desvio padrão.
Nesse caso foi o Atleta III é o mais regular (menor desvio padrão)
o Atleta II é o menos regular (maior desvio padrão).
Na terceira pesagem todos bateram o peso de 66kg e portanto aptos para lutar.
Então a primeira luta será entre os atletas II e III
Resposta C
Prova Matemática Enem 2016 comentada
QUESTÃO 141 – Enem 2016 prova azul
De forma geral, os pneus radiais trazem em sua lateral uma marcação do tipo abc/deRfg, como 185/65R15. Essa marcação identifica as medidas do pneu da seguinte forma:
- abc é a medida da largura do pneu, em milímetro;
- de é igual ao produto de 100 pela razão entre a medida da altura (em milímetro) e a medida da largura do pneu (em milímetro);
- R significa radial;
- fg é a medida do diâmetro interno do pneu, em polegada.
A figura ilustra as variáveis relacionadas com esses dados.
 O proprietário de um veículo precisa trocar os pneus de seu carro e, ao chegar a uma loja, é informado por um vendedor que há somente pneus com os seguintes códigos: 175/65R15, 175/75R15, 175/80R15, 185/60R15 e 205/55R15. Analisando, juntamente com o vendedor, as opções de pneus disponíveis, concluem que o pneu mais adequado para seu veículo é o que tem a menor altura.
Desta forma, o proprietário do veículo deverá comprar o pneu Com a marcação
a) 205/55R15.
b) 175/65R15.
c) 175/75R15.
d) 175/80R15.
e) 185/60R15.
Resolução
Sendo
H=altura e L=largura temos
de = 100. h/L
isolando h temos: h = de . L/100
a)h=55.205/100 =112,75 mm
b)h=65.175/100 = 113,75 mm
c)h=75.175/100 = 131,25 mm
d)H=80.175/100 = 140,00 mm
e)h=60.175/100 = 111,00 mm Menor altura
Resposta E
O proprietário de um veículo precisa trocar os pneus de seu carro e, ao chegar a uma loja, é informado por um vendedor que há somente pneus com os seguintes códigos: 175/65R15, 175/75R15, 175/80R15, 185/60R15 e 205/55R15. Analisando, juntamente com o vendedor, as opções de pneus disponíveis, concluem que o pneu mais adequado para seu veículo é o que tem a menor altura.
Desta forma, o proprietário do veículo deverá comprar o pneu Com a marcação
a) 205/55R15.
b) 175/65R15.
c) 175/75R15.
d) 175/80R15.
e) 185/60R15.
Resolução
Sendo
H=altura e L=largura temos
de = 100. h/L
isolando h temos: h = de . L/100
a)h=55.205/100 =112,75 mm
b)h=65.175/100 = 113,75 mm
c)h=75.175/100 = 131,25 mm
d)H=80.175/100 = 140,00 mm
e)h=60.175/100 = 111,00 mm Menor altura
Resposta E
Prova Matemática Enem 2016 comentada
QUESTÃO 142 – Enem 2016 prova azul
Uma família resolveu comprar um imóvel num bairro cujas ruas estão representadas na figura. As ruas com nomes de letras são paralelas entre si e perpendiculares às ruas identificadas com números. Todos os quarteirões são quadrados, com as mesmas medidas, e todas as ruas têm a mesma largura, permitindo caminhar somente nas direções vertical e horizontal. Desconsidere a largura das ruas.
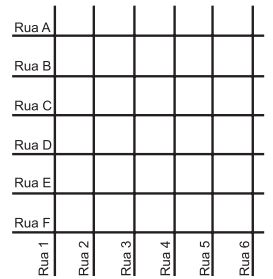 A família pretende que esse imóvel tenha a mesma distância de percurso até o local de trabalho da mãe, localizado na rua 6 com a rua E, o consultório do pai, na rua 2 com a rua E, e a escola das crianças, na rua 4 com a rua A. Com base nesses dados, o imóvel que atende as pretensões da família deverá ser localizado no encontro das ruas
a) 3 e C.
b) 4 e C.
c) 4 e D.
d) 4 e E.
e) 5 e C.
Resolução
A família pretende que esse imóvel tenha a mesma distância de percurso até o local de trabalho da mãe, localizado na rua 6 com a rua E, o consultório do pai, na rua 2 com a rua E, e a escola das crianças, na rua 4 com a rua A. Com base nesses dados, o imóvel que atende as pretensões da família deverá ser localizado no encontro das ruas
a) 3 e C.
b) 4 e C.
c) 4 e D.
d) 4 e E.
e) 5 e C.
Resolução
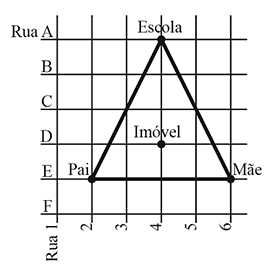 Nesse caso temos um triângulo isósceles e para que as 3 distâncias sejam iguais o imóvel deverá
estar a 3 quarteirões de cada um: consultório do pai, trabalho da mãe e escola. Isso acontece apenas no encontro das ruas 4 e D!
Resposta D
Nesse caso temos um triângulo isósceles e para que as 3 distâncias sejam iguais o imóvel deverá
estar a 3 quarteirões de cada um: consultório do pai, trabalho da mãe e escola. Isso acontece apenas no encontro das ruas 4 e D!
Resposta D
Prova Matemática Enem 2016 comentada
QUESTÃO 143 – Enem 2016 prova azul
Um senhor, pai de dois filhos, deseja comprar dois terrenos, com áreas de mesma medida, um para cada filho. Um dos terrenos visitados já está demarcado e, embora não tenha um formato convencional (como se observa na Figura B), agradou ao filho mais velho e, por isso, foi comprado. O filho mais novo possui um projeto arquitetônico de uma casa que quer construir, mas, para isso, precisa de um terreno na forma retangular (como mostrado na Figura A) cujo comprimento seja 7 m maior do que a largura.
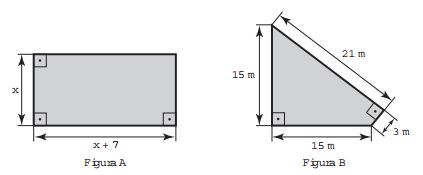 Para satisfazer o filho mais novo, esse senhor precisa encontrar um terreno retangular cujas medidas, em metro, do comprimento e da largura sejam iguais, respectivamente, a
a) 7,5 e 14,5.
b) 9,0 e 16,0.
c) 9,3 e 16,3.
d) 10,0 e 17,0.
e) 13,5 e 20,5.
Resolução
Para satisfazer o filho mais novo, esse senhor precisa encontrar um terreno retangular cujas medidas, em metro, do comprimento e da largura sejam iguais, respectivamente, a
a) 7,5 e 14,5.
b) 9,0 e 16,0.
c) 9,3 e 16,3.
d) 10,0 e 17,0.
e) 13,5 e 20,5.
Resolução
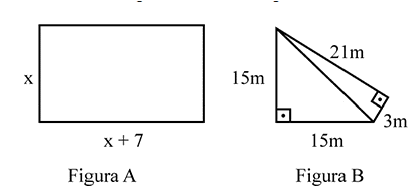 Na figura B temos 2 triângulos retângulos de área:
A = b1.h1/2 + b2.h2/2
A = 15.15/2 + 3.21/2
A = 144
Na figura A temos um retângulo de área:
A = b.h
144 = x(x+7)
X2 + 7x – 144 = 0
X = 9
Então as dimensões são: 9m e 16m
Resposta B
Na figura B temos 2 triângulos retângulos de área:
A = b1.h1/2 + b2.h2/2
A = 15.15/2 + 3.21/2
A = 144
Na figura A temos um retângulo de área:
A = b.h
144 = x(x+7)
X2 + 7x – 144 = 0
X = 9
Então as dimensões são: 9m e 16m
Resposta B
Prova Matemática Enem 2016 comentada
QUESTÃO 144 – Enem 2016 prova azul
Preocupada com seus resultados, uma empresa fez um balanço dos lucros obtidos nos últimos sete meses, conforme dados do quadro.
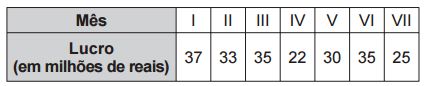 Avaliando os resultados, o conselho diretor da empresa decidiu comprar, nos dois meses subsequentes, a mesma quantidade de matéria-prima comprada no mês em que o lucro mais se aproximou da média dos lucros mensais dessa empresa nesse período de sete meses. Nos próximos dois meses, essa empresa deverá comprar a mesma quantidade de matéria- -prima comprada no mês
a) I.
b) II.
c) IV.
d) V.
e) VII
Resolução
Média de todos os meses (7 meses):
M = (37 + 33 + 35 + 22 + 30 + 35 + 25) / 7 = 31
O mês com o valor mais próximo da média foi o de valor 30!
Resposta D
Avaliando os resultados, o conselho diretor da empresa decidiu comprar, nos dois meses subsequentes, a mesma quantidade de matéria-prima comprada no mês em que o lucro mais se aproximou da média dos lucros mensais dessa empresa nesse período de sete meses. Nos próximos dois meses, essa empresa deverá comprar a mesma quantidade de matéria- -prima comprada no mês
a) I.
b) II.
c) IV.
d) V.
e) VII
Resolução
Média de todos os meses (7 meses):
M = (37 + 33 + 35 + 22 + 30 + 35 + 25) / 7 = 31
O mês com o valor mais próximo da média foi o de valor 30!
Resposta D
Prova Matemática Enem 2016 comentada
QUESTÃO 145 – Enem 2016 prova azul
O setor de recursos humanos de uma empresa pretende fazer contratações para adequar-se ao artigo 93 da Lei nº 8.213/91, que dispõe: Art. 93. A empresa com 100 (cem) ou mais empregados está obrigada a preencher de 2% (dois por cento) a 5% (cinco por cento) dos seus cargos com beneficiários reabilitados ou pessoas com deficiência, habilitadas, na seguinte proporção:
I. até 200 empregados……………….. 2%;
II. de 201 a 500 empregados…………… 3%;
III. de 501 a 1 000 empregados………… 4%;
IV. de 1 001 em diante………………. 5%.
Disponível em: www.planalto.gov.br. Acesso em: 3 fev. 2015.
Constatou-se que a empresa possui 1 200 funcionários, dos quais 10 são reabilitados ou com deficiência, habilitados. Para adequar-se à referida lei, a empresa contratará apenas empregados que atendem ao perfil indicado no artigo 93. O número mínimo de empregados reabilitados ou com deficiência, habilitados, que deverá ser contratado pela empresa é
a) 74.
b) 70.
c) 64.
d) 60.
e) 53.
Resolução
A empresa com 1200 funcionários se enquadra no nível IV
1200 + X __________________ 100%
10 + X ___________________5%
X = 52,6
Logo a empresa precisa contratar 53 Funcionários
Reasposta E
Prova Matemática Enem 2016 comentada
QUESTÃO 146 – Enem 2016 prova azul
Uma pessoa comercializa picolés. No segundo dia de certo evento ela comprou 4 caixas de picolés, pagando R$ 16,00 a caixa com 20 picolés para revendê-los no evento. No dia anterior, ela havia comprado a mesma quantidade de picolés, pagando a mesma quantia, e obtendo um lucro de R$ 40,00 (obtido exclusivamente pela diferença entre o valor de venda e o de compra dos picolés) com a venda de todos os picolés que possuía. Pesquisando o perfil do público que estará presente no evento, a pessoa avalia que será possível obter um lucro 20% maior do que o obtido com a venda no primeiro dia do evento. Para atingir seu objetivo, e supondo que todos os picolés disponíveis foram vendidos no segundo dia, o valor de venda de cada picolé, no segundo dia, deve ser
a) R$ 0,96.
b) R$ 1,00.
c) R$ 1,40.
d) R$ 1,50.
e) R$ 1,56.
Resposta C
Resolução
Lucro do primeiro dia = R$40
Lucro do segundo dia = R$40 x 1,2 = R$48
Lucro por caixa = 48/4 = R$12
Foi vendido 12 + 16 = R$ 28,00
28/20 = 1,4
Resposta C
Prova Matemática Enem 2016 comentada
QUESTÃO 147 – Enem 2016 prova azul
O tênis é um esporte em que a estratégia de jogo a ser adotada depende, entre outros fatores, de o adversário ser canhoto ou destro. Um clube tem um grupo de 10 tenistas, sendo que 4 são canhotos e 6 são destros. O técnico do clube deseja realizar uma partida de exibição entre dois desses jogadores, porém, não poderão ser ambos canhotos. Qual o número de possibilidades de escolha dos tenistas para a partida de exibição?
a) 10!/(2!x8!) – 4!/(2!x2!)
b) 10!/8! – 4!/2!
c) 10!/2!x8! – 2
d) 6!/4! + 4×4
e) 6!/4! + 6×4
Resolução
O número de possibilidades de escolher dois tenistas com a condição de que ambos não possam ser canhotos é dado pelo total de maneiras de se escolher dois jogadores dentre os dez possíveis menos o total de maneiras de se escolher dois jogadores dentre os quatro canhotos:
C10,2 – C4,2 = 10!/(2!x8!) – 4!/(2!x2!)
Resposta A
Prova Matemática Enem 2016 comentada
QUESTÃO 148 – Enem 2016 prova azul
O ábaco é um antigo instrumento de cálculo que usa notação posicional de base dez para representar números naturais. Ele pode ser apresentado em vários modelos, um deles é formado por hastes apoiadas em uma base. Cada haste corresponde a uma posição no sistema decimal e nelas são colocadas argolas; a quantidade de argolas na haste representa o algarismo daquela posição. Em geral, colocam-se adesivos abaixo das hastes com os símbolos U, D, C, M, DM e CM que correspondem, respectivamente, a unidades, dezenas, centenas, unidades de milhar, dezenas de milhar e centenas de milhar, sempre começando com a unidade na haste da direita e as demais ordens do número no sistema decimal nas hastes subsequentes (da direita para esquerda), até a haste que se encontra mais à esquerda. Entretanto, no ábaco da figura, os adesivos não seguiram a disposição usual.
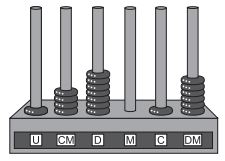 Nessa disposição, o número que está representado na figura é
a) 46 171.
b) 147 016.
c) 171 064.
d) 460 171.
e) 610 741.
Resolução
O número de argolas nas hastes referentes a CM, DM, M, C, D e U são 4, 6, 0, 1, 7 e 1, respectivamente. Portanto o número representado é 460 171.
Resposta D
Nessa disposição, o número que está representado na figura é
a) 46 171.
b) 147 016.
c) 171 064.
d) 460 171.
e) 610 741.
Resolução
O número de argolas nas hastes referentes a CM, DM, M, C, D e U são 4, 6, 0, 1, 7 e 1, respectivamente. Portanto o número representado é 460 171.
Resposta D
Prova Matemática Enem 2016 comentada
QUESTÃO 149 – Enem 2016 prova azul
Para uma feira de ciências, dois projéteis de foguetes, A e B, estão sendo construídos para serem lançados. O planejamento é que eles sejam lançados juntos, com o objetivo de o projétil B interceptar o A quando esse alcançar sua altura máxima. Para que isso aconteça, um dos projéteis descreverá uma trajetória parabólica, enquanto o outro irá descrever uma trajetória supostamente retilínea. O gráfico mostra as alturas alcançadas por esses projéteis em função do tempo, nas simulações realizadas.
 Com base nessas simulações, observou-se que a trajetória do projétil B deveria ser alterada para que o objetivo fosse alcançado.
Para alcançar o objetivo, o coeficiente angular da reta que representa a trajetória de B deverá
a) diminuir em 2 unidades.
b) diminuir em 4 unidades.
c) aumentar em 2 unidades.
d) aumentar em 4 unidades.
e) aumentar em 8 unidades.
Resolução
Originalmente, a trajetória do projétil B passa pelos pontos (0, 0) e (2, 4), como visto no gráfico. Logo, seu coeficiente angular é:
Com base nessas simulações, observou-se que a trajetória do projétil B deveria ser alterada para que o objetivo fosse alcançado.
Para alcançar o objetivo, o coeficiente angular da reta que representa a trajetória de B deverá
a) diminuir em 2 unidades.
b) diminuir em 4 unidades.
c) aumentar em 2 unidades.
d) aumentar em 4 unidades.
e) aumentar em 8 unidades.
Resolução
Originalmente, a trajetória do projétil B passa pelos pontos (0, 0) e (2, 4), como visto no gráfico. Logo, seu coeficiente angular é:
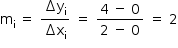 Como a trajetória do projétil B deve encontrar a trajetória do projétil A em sua altura máxima, o projétil B deve partir da origem (0, 0) e passar pelo ponto (4, 16), no qual A tem sua altura máxima. Logo, o coeficiente angular será:
Como a trajetória do projétil B deve encontrar a trajetória do projétil A em sua altura máxima, o projétil B deve partir da origem (0, 0) e passar pelo ponto (4, 16), no qual A tem sua altura máxima. Logo, o coeficiente angular será:
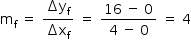 A diferença entre ambos os coeficientes é, portanto, de:
A diferença entre ambos os coeficientes é, portanto, de:
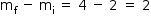 Ou seja, deve aumentar em 2 unidades.
Resposta D
Ou seja, deve aumentar em 2 unidades.
Resposta D
Prova Matemática Enem 2016 comentada
Veja aqui a correção da prova de Matemática do segundo dia. Prova Matemática Enem 2016 comentada !
QUESTÃO 136 – Enem 2016 prova azul
Em regiões agrícolas, é comum a presença de silos para armazenamento e secagem da produção de grãos, no formato de um cilindro reto, sobreposto por um cone, e dimensões indicadas na figura. O silo fica cheio e o transporte dos grãos é feito em caminhões de carga cuja capacidade é de 20 m3. Uma região possui um silo cheio e apenas um caminhão para transportar os grãos para a usina de beneficiamento.

Utilize 3 como aproximação para π.
O número mínimo de viagens que o caminhão precisará fazer para transportar todo o volume de grãos armazenados no Silo é
a) 6.
b) 16.
c) 17.
d) 18.
e) 21.
Resolução Questão 136 – Prova Azul
Vsilo = Vcilindro + Vcone
Vsilo = Ab.h +Ab.h/3 =
Vsilo = π.Rci2.h + π.Rco2.h/3
Vsilo = π.32.12 + π.32.3/3 =
Vsilo = 117 π =
Vsilo = 117.3 = 351
Número de viagens = 351/20 = 17,55 ≈18
Resposta D
Prova Matemática Enem 2016 comentada
QUESTÃO 137 – Enem 2016 prova azul
Em uma empresa de móveis, um cliente encomenda um guarda-roupa nas dimensões 220 cm de altura, 120 cm de largura e 50 cm de profundidade. Alguns dias depois, o projetista, com o desenho elaborado na escala 1 : 8, entra em contato com o cliente para fazer sua apresentação. No momento da impressão, o profissional percebe que o desenho não caberia na folha de papel que costumava usar. Para resolver o problema, configurou a impressora para que a figura fosse reduzida em 20%.
A altura, a largura e a profundidade do desenho impresso para a apresentação serão, respectivamente,
a) 22,00 cm, 12,00 cm e 5,00 cm.
b) 27,50 cm, 15,00 cm e 6,25 cm.
c) 34,37 cm, 18,75 cm e 7,81 cm.
d) 35,20 cm, 19,20 cm e 8,00 cm.
e) 44,00 cm, 24,00 cm e 10.00 cm.
Resolução Questão 137 – Prova Azul
Inicialmente, ao elaborar o desenho na escala 1 : 8, dividem-se todas as medidas por 8. Em seguida, reduz-se a figura em 20%, o que é equivalente a multiplicar as medidas por 0,8. Assim, as medidas finais do desenho são:
Real:
Altura = h = 220cm
Largura = L = 120cm
Profundidade = P = 50cm
Escala 1:8
Desenho:
h = 220cm/8 = 27,5
L = 120/8 = 15
P = 50/8=6,25
Redução 20%:
h = 27,5 . 0,8 = 22 cm
L = 15 . 0,8 = 12 cm
P = 6,25 . 0,8 = 5 cm
Resposta A
Prova Matemática Enem 2016 comentada
QUESTÃO 138 – Enem 2016 prova azul
A London Eye é uma enorme roda-gigante na capital inglesa. Por ser um dos monumentos construídos para celebrar a entrada do terceiro milênio, ela também é conhecida como Roda do Milênio. Um turista brasileiro, em visita à Inglaterra, perguntou a um londrino o diâmetro (destacado na imagem) da Roda do Milênio e ele respondeu que ele tem 443 pés.

Disponível em: www.mapadelondres.org. Acesso em 14 maio 2015 (adaptado).
Não habituado com a unidade pé, e querendo satisfazer sua curiosidade, esse turista consultou um manual de unidades de medidas e constatou que 1 pé equivale a 12 polegadas, e que 1 polegada equivale a 2,54 cm. Após alguns cálculos de conversão, o turista ficou surpreendido com o resultado obtido em metros.
Qual a medida que mais se aproxima do diâmetro da Roda do Milênio, em metro?
a) 53
b) 94
c) 113
d) 135
e) 145
Resolução Questão 138 – Prova Azul
Diâmetro = 443 pés
Diâmetro = 443 . 12 = 5316 polegadas
Diâmetro = 5316 . 2,54cm
Diâmetro ≈ 13502 cm
Diâmetro ≈ 135,02 m
Resposta D
Prova Matemática Enem 2016 comentada
QUESTÃO 139- Enem 2016 prova azul
Uma cisterna de 6 000 L foi esvaziada em um período de 3 h. Na primeira hora foi utilizada apenas uma bomba, mas nas duas horas seguintes, a fim de reduzir o tempo de esvaziamento, outra bomba foi ligada junto com a primeira. O gráfico, formado por dois segmentos de reta, mostra o volume de água presente na cisterna, em função do tempo.

Qual é a vazão, em litro por hora, da bomba que foi ligada no início da segunda hora?
a) 1 000
b) 1 250
c) 1 500
d) 2 000
e) 2 500
Resolução
Do gráfico, sendo V1 a vazão da bomba ligada primeiro e V2 a da aberta ao fim da primeira hora, tem-se:
Bomba 1
Vazão = ∆y/ ∆x
Vazão = 1000/1 = 1000
Bomba 1 e 2
Vazão = ∆y/ ∆x
Vazão = 5000/2 = 2500
Logo a vazão da bomba 2 é:
2500 – 1000 = 1500 L/h
Resposta C
Prova Matemática Enem 2016 comentada
QUESTÃO 140- Enem 2016 prova azul
O procedimento de perda rápida de “peso” é comum entre os atletas dos esportes de combate. Para participar de um torneio, quatro atletas da categoria até 66 kg, Peso-Pena, foram submetidos a dietas balanceadas e atividades físicas. Realizaram três “pesagens” antes do início do torneio. Pelo regulamento do torneio, a primeira luta deverá ocorrer entre o atleta mais regular e o menos regular quanto aos “pesos”. As informações com base nas pesagens dos atletas estão no quadro.

Após as três “pesagens”, os organizadores do torneio informaram aos atletas quais deles se enfrentariam na primeira luta.
A primeira luta foi entre os atletas
a) I e III.
b) I e IV.
c) II e III.
d) II e IV.
e) III e IV.
Resolução
Em casos de empate, o atleta de melhor desempenho e mais regular é aquele que não se afasta da média ou seja o de menor desvio padrão.
Nesse caso foi o Atleta III é o mais regular (menor desvio padrão)
o Atleta II é o menos regular (maior desvio padrão).
Na terceira pesagem todos bateram o peso de 66kg e portanto aptos para lutar.
Então a primeira luta será entre os atletas II e III
Resposta C
Prova Matemática Enem 2016 comentada
QUESTÃO 141 – Enem 2016 prova azul
De forma geral, os pneus radiais trazem em sua lateral uma marcação do tipo abc/deRfg, como 185/65R15. Essa marcação identifica as medidas do pneu da seguinte forma:
A figura ilustra as variáveis relacionadas com esses dados.

O proprietário de um veículo precisa trocar os pneus de seu carro e, ao chegar a uma loja, é informado por um vendedor que há somente pneus com os seguintes códigos: 175/65R15, 175/75R15, 175/80R15, 185/60R15 e 205/55R15. Analisando, juntamente com o vendedor, as opções de pneus disponíveis, concluem que o pneu mais adequado para seu veículo é o que tem a menor altura.
Desta forma, o proprietário do veículo deverá comprar o pneu Com a marcação
a) 205/55R15.
b) 175/65R15.
c) 175/75R15.
d) 175/80R15.
e) 185/60R15.
Resolução
Sendo
H=altura e L=largura temos
de = 100. h/L
isolando h temos: h = de . L/100
a)h=55.205/100 =112,75 mm
b)h=65.175/100 = 113,75 mm
c)h=75.175/100 = 131,25 mm
d)H=80.175/100 = 140,00 mm
e)h=60.175/100 = 111,00 mm Menor altura
Resposta E
Prova Matemática Enem 2016 comentada
QUESTÃO 142 – Enem 2016 prova azul
Uma família resolveu comprar um imóvel num bairro cujas ruas estão representadas na figura. As ruas com nomes de letras são paralelas entre si e perpendiculares às ruas identificadas com números. Todos os quarteirões são quadrados, com as mesmas medidas, e todas as ruas têm a mesma largura, permitindo caminhar somente nas direções vertical e horizontal. Desconsidere a largura das ruas.

A família pretende que esse imóvel tenha a mesma distância de percurso até o local de trabalho da mãe, localizado na rua 6 com a rua E, o consultório do pai, na rua 2 com a rua E, e a escola das crianças, na rua 4 com a rua A. Com base nesses dados, o imóvel que atende as pretensões da família deverá ser localizado no encontro das ruas
a) 3 e C.
b) 4 e C.
c) 4 e D.
d) 4 e E.
e) 5 e C.
Resolução

Nesse caso temos um triângulo isósceles e para que as 3 distâncias sejam iguais o imóvel deverá
estar a 3 quarteirões de cada um: consultório do pai, trabalho da mãe e escola. Isso acontece apenas no encontro das ruas 4 e D!
Resposta D
Prova Matemática Enem 2016 comentada
QUESTÃO 143 – Enem 2016 prova azul
Um senhor, pai de dois filhos, deseja comprar dois terrenos, com áreas de mesma medida, um para cada filho. Um dos terrenos visitados já está demarcado e, embora não tenha um formato convencional (como se observa na Figura B), agradou ao filho mais velho e, por isso, foi comprado. O filho mais novo possui um projeto arquitetônico de uma casa que quer construir, mas, para isso, precisa de um terreno na forma retangular (como mostrado na Figura A) cujo comprimento seja 7 m maior do que a largura.

Para satisfazer o filho mais novo, esse senhor precisa encontrar um terreno retangular cujas medidas, em metro, do comprimento e da largura sejam iguais, respectivamente, a
a) 7,5 e 14,5.
b) 9,0 e 16,0.
c) 9,3 e 16,3.
d) 10,0 e 17,0.
e) 13,5 e 20,5.
Resolução

Na figura B temos 2 triângulos retângulos de área:
A = b1.h1/2 + b2.h2/2
A = 15.15/2 + 3.21/2
A = 144
Na figura A temos um retângulo de área:
A = b.h
144 = x(x+7)
X2 + 7x – 144 = 0
X = 9
Então as dimensões são: 9m e 16m
Resposta B
Prova Matemática Enem 2016 comentada
QUESTÃO 144 – Enem 2016 prova azul
Preocupada com seus resultados, uma empresa fez um balanço dos lucros obtidos nos últimos sete meses, conforme dados do quadro.

Avaliando os resultados, o conselho diretor da empresa decidiu comprar, nos dois meses subsequentes, a mesma quantidade de matéria-prima comprada no mês em que o lucro mais se aproximou da média dos lucros mensais dessa empresa nesse período de sete meses. Nos próximos dois meses, essa empresa deverá comprar a mesma quantidade de matéria- -prima comprada no mês
a) I.
b) II.
c) IV.
d) V.
e) VII
Resolução
Média de todos os meses (7 meses):
M = (37 + 33 + 35 + 22 + 30 + 35 + 25) / 7 = 31
O mês com o valor mais próximo da média foi o de valor 30!
Resposta D
Prova Matemática Enem 2016 comentada
QUESTÃO 145 – Enem 2016 prova azul
O setor de recursos humanos de uma empresa pretende fazer contratações para adequar-se ao artigo 93 da Lei nº 8.213/91, que dispõe: Art. 93. A empresa com 100 (cem) ou mais empregados está obrigada a preencher de 2% (dois por cento) a 5% (cinco por cento) dos seus cargos com beneficiários reabilitados ou pessoas com deficiência, habilitadas, na seguinte proporção:
I. até 200 empregados……………….. 2%;
II. de 201 a 500 empregados…………… 3%;
III. de 501 a 1 000 empregados………… 4%;
IV. de 1 001 em diante………………. 5%.
Disponível em: www.planalto.gov.br. Acesso em: 3 fev. 2015.
Constatou-se que a empresa possui 1 200 funcionários, dos quais 10 são reabilitados ou com deficiência, habilitados. Para adequar-se à referida lei, a empresa contratará apenas empregados que atendem ao perfil indicado no artigo 93. O número mínimo de empregados reabilitados ou com deficiência, habilitados, que deverá ser contratado pela empresa é
a) 74.
b) 70.
c) 64.
d) 60.
e) 53.
Resolução
A empresa com 1200 funcionários se enquadra no nível IV
1200 + X __________________ 100%
10 + X ___________________5%
X = 52,6
Logo a empresa precisa contratar 53 Funcionários
Reasposta E
Prova Matemática Enem 2016 comentada
QUESTÃO 146 – Enem 2016 prova azul
Uma pessoa comercializa picolés. No segundo dia de certo evento ela comprou 4 caixas de picolés, pagando R$ 16,00 a caixa com 20 picolés para revendê-los no evento. No dia anterior, ela havia comprado a mesma quantidade de picolés, pagando a mesma quantia, e obtendo um lucro de R$ 40,00 (obtido exclusivamente pela diferença entre o valor de venda e o de compra dos picolés) com a venda de todos os picolés que possuía. Pesquisando o perfil do público que estará presente no evento, a pessoa avalia que será possível obter um lucro 20% maior do que o obtido com a venda no primeiro dia do evento. Para atingir seu objetivo, e supondo que todos os picolés disponíveis foram vendidos no segundo dia, o valor de venda de cada picolé, no segundo dia, deve ser
a) R$ 0,96.
b) R$ 1,00.
c) R$ 1,40.
d) R$ 1,50.
e) R$ 1,56.
Resposta C
Resolução
Lucro do primeiro dia = R$40
Lucro do segundo dia = R$40 x 1,2 = R$48
Lucro por caixa = 48/4 = R$12
Foi vendido 12 + 16 = R$ 28,00
28/20 = 1,4
Resposta C
Prova Matemática Enem 2016 comentada
QUESTÃO 147 – Enem 2016 prova azul
O tênis é um esporte em que a estratégia de jogo a ser adotada depende, entre outros fatores, de o adversário ser canhoto ou destro. Um clube tem um grupo de 10 tenistas, sendo que 4 são canhotos e 6 são destros. O técnico do clube deseja realizar uma partida de exibição entre dois desses jogadores, porém, não poderão ser ambos canhotos. Qual o número de possibilidades de escolha dos tenistas para a partida de exibição?
a) 10!/(2!x8!) – 4!/(2!x2!)
b) 10!/8! – 4!/2!
c) 10!/2!x8! – 2
d) 6!/4! + 4×4
e) 6!/4! + 6×4
Resolução
O número de possibilidades de escolher dois tenistas com a condição de que ambos não possam ser canhotos é dado pelo total de maneiras de se escolher dois jogadores dentre os dez possíveis menos o total de maneiras de se escolher dois jogadores dentre os quatro canhotos:
C10,2 – C4,2 = 10!/(2!x8!) – 4!/(2!x2!)
Resposta A
Prova Matemática Enem 2016 comentada
QUESTÃO 148 – Enem 2016 prova azul
O ábaco é um antigo instrumento de cálculo que usa notação posicional de base dez para representar números naturais. Ele pode ser apresentado em vários modelos, um deles é formado por hastes apoiadas em uma base. Cada haste corresponde a uma posição no sistema decimal e nelas são colocadas argolas; a quantidade de argolas na haste representa o algarismo daquela posição. Em geral, colocam-se adesivos abaixo das hastes com os símbolos U, D, C, M, DM e CM que correspondem, respectivamente, a unidades, dezenas, centenas, unidades de milhar, dezenas de milhar e centenas de milhar, sempre começando com a unidade na haste da direita e as demais ordens do número no sistema decimal nas hastes subsequentes (da direita para esquerda), até a haste que se encontra mais à esquerda. Entretanto, no ábaco da figura, os adesivos não seguiram a disposição usual.

Nessa disposição, o número que está representado na figura é
a) 46 171.
b) 147 016.
c) 171 064.
d) 460 171.
e) 610 741.
Resolução
O número de argolas nas hastes referentes a CM, DM, M, C, D e U são 4, 6, 0, 1, 7 e 1, respectivamente. Portanto o número representado é 460 171.
Resposta D
Prova Matemática Enem 2016 comentada
QUESTÃO 149 – Enem 2016 prova azul
Para uma feira de ciências, dois projéteis de foguetes, A e B, estão sendo construídos para serem lançados. O planejamento é que eles sejam lançados juntos, com o objetivo de o projétil B interceptar o A quando esse alcançar sua altura máxima. Para que isso aconteça, um dos projéteis descreverá uma trajetória parabólica, enquanto o outro irá descrever uma trajetória supostamente retilínea. O gráfico mostra as alturas alcançadas por esses projéteis em função do tempo, nas simulações realizadas.

Com base nessas simulações, observou-se que a trajetória do projétil B deveria ser alterada para que o objetivo fosse alcançado.
Para alcançar o objetivo, o coeficiente angular da reta que representa a trajetória de B deverá
a) diminuir em 2 unidades.
b) diminuir em 4 unidades.
c) aumentar em 2 unidades.
d) aumentar em 4 unidades.
e) aumentar em 8 unidades.
Resolução
Originalmente, a trajetória do projétil B passa pelos pontos (0, 0) e (2, 4), como visto no gráfico. Logo, seu coeficiente angular é:
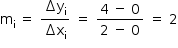
Como a trajetória do projétil B deve encontrar a trajetória do projétil A em sua altura máxima, o projétil B deve partir da origem (0, 0) e passar pelo ponto (4, 16), no qual A tem sua altura máxima. Logo, o coeficiente angular será:
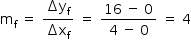
A diferença entre ambos os coeficientes é, portanto, de:
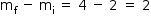
Ou seja, deve aumentar em 2 unidades.
Resposta D
Prova Matemática Enem 2016 comentada
Questão 150
Para a construção de isolamento acústico numa parede cuja área mede 9 m2, sabe-se que, se a fonte sonora estiver a 3 m do plano da parede, o custo é de R$ 500,00. Nesse tipo de isolamento, a espessura do material que reveste a parede é inversamente proporcional ao quadrado da distância até a fonte sonora, e o custo é diretamente proporcional ao volume do material do revestimento.
Uma expressão que fornece o custo para revestir uma parede de área A (em metro quadrado), situada a D metros da fonte sonora, é
a) 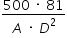 b)
b)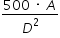 c)
c)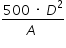 d)
d) e)
e)
Para a construção de isolamento acústico numa parede cuja área mede 9 m2, sabe-se que, se a fonte sonora estiver a 3 m do plano da parede, o custo é de R$ 500,00. Nesse tipo de isolamento, a espessura do material que reveste a parede é inversamente proporcional ao quadrado da distância até a fonte sonora, e o custo é diretamente proporcional ao volume do material do revestimento.
Uma expressão que fornece o custo para revestir uma parede de área A (em metro quadrado), situada a D metros da fonte sonora, é
a) 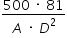
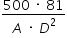
b)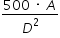
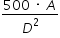
c)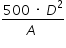
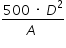
d)

e)

Resolução
Sejam E a espessura, C o custo e V o volume.
A e E são diretamente proporcionais a V.
Como C é diretamente proporcional a V (enunciado), C é diretamente proporcional a A.
Como E é inversamente proporcional a D2 (enunciado), C é inversamente proporcional a D2.
Então 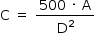 .
Resposta B
.
Resposta B
Prova Matemática Enem 2016 comentada
Sejam E a espessura, C o custo e V o volume.
A e E são diretamente proporcionais a V.
Como C é diretamente proporcional a V (enunciado), C é diretamente proporcional a A.
Como E é inversamente proporcional a D2 (enunciado), C é inversamente proporcional a D2.
Então 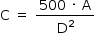 .
.
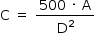 .
.
Resposta B
Prova Matemática Enem 2016 comentada
Questão 151
A fim de acompanhar o crescimento de crianças, foram criadas pela Organização Mundial da Saúde (OMS) tabelas de altura, também adotadas pelo Ministério da Saúde do Brasil. Além de informar os dados referentes ao índice de crescimento, a tabela traz gráficos com curvas, apresentando padrões de crescimento estipulados pela OMS.
O gráfico apresenta o crescimento de meninas, cuja análise se dá pelo ponto de intersecção entre o comprimento, em centímetro, e a idade, em mês completo e ano, da criança.
 Disponível em: www.aprocura.com.br. Acesso em: 22 out. 2015 (adaptado).
Uma menina aos 3 anos de idade tinha altura de 85 centímetros e aos 4 anos e 4 meses sua altura chegou a um valor que corresponde a um ponto exatamente sobre a curva p50.
Qual foi o aumento percentual da altura dessa menina, descrito com uma casa decimal, no período considerado?
a) 23,5%
b) 21,2%
c) 19,0%
d) 11,8%
e) 10,0%
Resolução
Pelo enunciado da questão, traçou-se um segmento conforme o gráfico abaixo.
Disponível em: www.aprocura.com.br. Acesso em: 22 out. 2015 (adaptado).
Uma menina aos 3 anos de idade tinha altura de 85 centímetros e aos 4 anos e 4 meses sua altura chegou a um valor que corresponde a um ponto exatamente sobre a curva p50.
Qual foi o aumento percentual da altura dessa menina, descrito com uma casa decimal, no período considerado?
a) 23,5%
b) 21,2%
c) 19,0%
d) 11,8%
e) 10,0%
Resolução
Pelo enunciado da questão, traçou-se um segmento conforme o gráfico abaixo.
 A variação da altura é de 105 – 85 = 20 cm.
A porcentagem da variação é calculada por:
A variação da altura é de 105 – 85 = 20 cm.
A porcentagem da variação é calculada por:
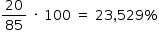 Com uma casa decimal: 23,5%
Resposta A
Com uma casa decimal: 23,5%
Resposta A
Prova Matemática Enem 2016 comentada
A fim de acompanhar o crescimento de crianças, foram criadas pela Organização Mundial da Saúde (OMS) tabelas de altura, também adotadas pelo Ministério da Saúde do Brasil. Além de informar os dados referentes ao índice de crescimento, a tabela traz gráficos com curvas, apresentando padrões de crescimento estipulados pela OMS.
O gráfico apresenta o crescimento de meninas, cuja análise se dá pelo ponto de intersecção entre o comprimento, em centímetro, e a idade, em mês completo e ano, da criança.

Disponível em: www.aprocura.com.br. Acesso em: 22 out. 2015 (adaptado).
Uma menina aos 3 anos de idade tinha altura de 85 centímetros e aos 4 anos e 4 meses sua altura chegou a um valor que corresponde a um ponto exatamente sobre a curva p50.
Qual foi o aumento percentual da altura dessa menina, descrito com uma casa decimal, no período considerado?
a) 23,5%
b) 21,2%
c) 19,0%
d) 11,8%
e) 10,0%
Resolução
Pelo enunciado da questão, traçou-se um segmento conforme o gráfico abaixo.

A variação da altura é de 105 – 85 = 20 cm.
A porcentagem da variação é calculada por:
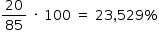
Com uma casa decimal: 23,5%
Resposta A
Prova Matemática Enem 2016 comentada
Prova Matemática Enem 2016 comentada
QUESTÃO 152 – Enem 2016 prova azul
Um adolescente vai a um parque de diversões tendo, prioritariamente, o desejo de ir a um brinquedo que se encontra na área IV, dentre as áreas I, II, III, IV e V existentes. O esquema ilustra o mapa do parque, com a localização da entrada, das cinco áreas com os brinquedos disponíveis e dos possíveis caminhos para se chegar a cada área. O adolescente não tem conhecimento do mapa do parque e decide ir caminhando da entrada até chegar à área IV.
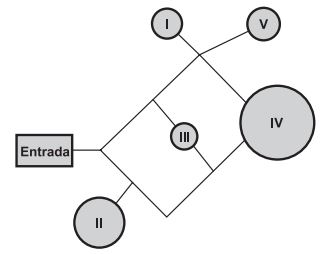 Suponha que relativamente a cada ramificação, as opções existentes de percurso pelos caminhos apresentem iguais probabilidades de escolha, que a caminhada foi feita escolhendo ao acaso os caminhos existentes e que, ao tomar um caminho que chegue a uma área distinta da IV, o adolescente necessariamente passa por ela ou retorna. Nessas condições, a probabilidade de ele chegar à área IV sem passar por outras áreas e sem retornar é igual a
a) 1/96
b) 1/64
c) 5/24
d) 1/ 4
e) 5/12
Resolução
Sendo A, B, C, D e E as ramificações como mostradas no desenho anterior, temos apenas dois caminhos sem passar por outras áreas e sem retornar: entrada ” A ” B ” C ” IV e entrada ” A ” D ” E ” IV. Sendo o primeiro com probabilidade 1/2 . 1/2 . 1/3 = 1 /12 e o segundo com probabilidade 1/2 . 1/2 . 1/2 = 1/8
Sendo assim a probabilidade é 1/12 + 1/8 = 5/24
Resposta C
Suponha que relativamente a cada ramificação, as opções existentes de percurso pelos caminhos apresentem iguais probabilidades de escolha, que a caminhada foi feita escolhendo ao acaso os caminhos existentes e que, ao tomar um caminho que chegue a uma área distinta da IV, o adolescente necessariamente passa por ela ou retorna. Nessas condições, a probabilidade de ele chegar à área IV sem passar por outras áreas e sem retornar é igual a
a) 1/96
b) 1/64
c) 5/24
d) 1/ 4
e) 5/12
Resolução
Sendo A, B, C, D e E as ramificações como mostradas no desenho anterior, temos apenas dois caminhos sem passar por outras áreas e sem retornar: entrada ” A ” B ” C ” IV e entrada ” A ” D ” E ” IV. Sendo o primeiro com probabilidade 1/2 . 1/2 . 1/3 = 1 /12 e o segundo com probabilidade 1/2 . 1/2 . 1/2 = 1/8
Sendo assim a probabilidade é 1/12 + 1/8 = 5/24
Resposta C
Prova Matemática Enem 2016 comentada
QUESTÃO 153 – Enem 2016 prova azul
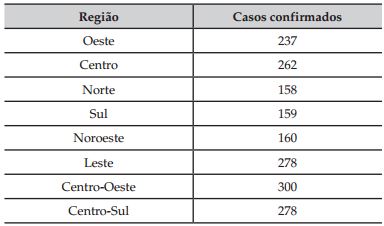
Em uma cidade, o número de casos de dengue confirmados aumentou consideravelmente nos últimos dias. A prefeitura resolveu desenvolver uma ação contratando funcionários para ajudar no combate à doença, os quais orientarão os moradores a eliminarem criadouros do mosquito Aedes aegypti, transmissor da dengue. A tabela apresenta o número atual de casos confirmados, por região da cidade.
 A prefeitura optou pela seguinte distribuição dos funcionários a serem contratados:
I. 10 funcionários para cada região da cidade cujo número de casos seja maior que a média dos casos confirmados.
II. 7 funcionários para cada região da cidade cujo número de casos seja menor ou igual à média dos casos confirmados.
Quantos funcionários a prefeitura deverá contratar para efetivar a ação?
a) 59
b) 65
c) 68
d) 71
e) 80
Resolução
A média de casos confirmados é dada por
M = (237 + 262 + 158 + 159 + 160 + 278 + 300 + 278) /8 = 229
Das oito regiões da cidade, cinco delas (oeste, centro, leste, centro-oeste e centro-sul) estão acima da média, isto é, cada uma delas receberá 10 funcionários; três regiões estão abaixo da média (norte, sul e noroeste) e cada uma delas receberá 7 funcionários. Portanto, a prefeitura deverá contratar 5 ⋅ 10 + 3 ⋅ 7 = 71 funcionários.
Resposta D
A prefeitura optou pela seguinte distribuição dos funcionários a serem contratados:
I. 10 funcionários para cada região da cidade cujo número de casos seja maior que a média dos casos confirmados.
II. 7 funcionários para cada região da cidade cujo número de casos seja menor ou igual à média dos casos confirmados.
Quantos funcionários a prefeitura deverá contratar para efetivar a ação?
a) 59
b) 65
c) 68
d) 71
e) 80
Resolução
A média de casos confirmados é dada por
M = (237 + 262 + 158 + 159 + 160 + 278 + 300 + 278) /8 = 229
Das oito regiões da cidade, cinco delas (oeste, centro, leste, centro-oeste e centro-sul) estão acima da média, isto é, cada uma delas receberá 10 funcionários; três regiões estão abaixo da média (norte, sul e noroeste) e cada uma delas receberá 7 funcionários. Portanto, a prefeitura deverá contratar 5 ⋅ 10 + 3 ⋅ 7 = 71 funcionários.
Resposta D
Prova Matemática Enem 2016 comentada
QUESTÃO 154- Enem 2016 prova azul
Cinco marcas de pão integral apresentam as seguintes concentrações de fibras (massa de fibra por massa de pão):
• Marca A: 2 g de fibras a cada 50 g de pão;
• Marca B: 5 g de fibras a cada 40 g de pão;
• Marca C: 5 g de fibras a cada 100 g de pão;
• Marca D: 6 g de fibras a cada 90 g de pão;
• Marca E: 7 g de fibras a cada 70 g de pão.
Recomenda-se a ingestão do pão que possui a maior concentração de fibras. Disponível em: www.blog.saude.gov.br. Acesso em: 25 fev. 2013. A marca a ser escolhida é
a) A.
b) B.
c) C.
d) D.
e) E.
Resolução
Deverá ser escolhida a marca de pão que apresenta a maior razão entre a massa de fibra e a massa de pão. Sendo A, B, C, D e E as razões respectivas de cada marca de pão:
• A = 2/ 50 = 0 040
• B = 5/40 = 0125
• C = 5/100 = 0 050
• D 6/ 90 = 0 066
• E 7/70 = 0100
Como A < C < D < E < B, a marca de pão que escolhida é a B
Resposta B
Prova Matemática Enem 2016 comentada
QUESTÃO 155- Enem 2016 prova azul
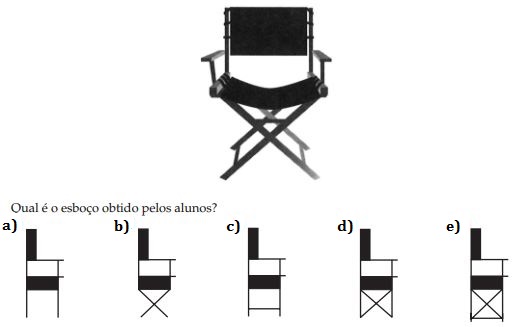
Os alunos de uma escola utilizaram cadeiras iguais às da figura para uma aula ao ar livre. A professora, ao final da aula, solicitou que os alunos fechassem as cadeiras para guardá-las. Depois de guardadas, os alunos fizeram um esboço da vista lateral da cadeira fechada.
 Resolução
A melhor representação lateral é da letra C
Resposta C
QUESTÃO 156- Enem 2016 prova azul
Para garantir a segurança de um grande evento público que terá início às 4 h da tarde, um organizador precisa monitorar a quantidade de pessoas presentes em cada instante. Para cada 2 000 pessoas se faz necessária a presença de um policial. Além disso, estima-se uma densidade de quatro pessoas por metro quadrado de área de terreno ocupado. Às 10 h da manhã, o organizador verifica que a área de terreno já ocupada equivale a um quadrado com lados medindo 500 m. Porém, nas horas seguintes, espera-se que o público aumente a uma taxa de 120 000 pessoas por hora até o início do evento, quando não será mais permitida a entrada de público. Quantos policiais serão necessários no início do evento para garantir a segurança?
a) 360
b) 485
c) 560
d) 740
e) 860
Resolução
Às 10 horas da manhã havia 4 ⋅ 5002 = 1 000 000 de pessoas presentes e até as 4 horas da tarde chegarão mais 120 000 ⋅ 6 = 720 000 pessoas. Portanto, serão necessários 1720 000 / 2000= 860 policiais
Resposta E
Resolução
A melhor representação lateral é da letra C
Resposta C
QUESTÃO 156- Enem 2016 prova azul
Para garantir a segurança de um grande evento público que terá início às 4 h da tarde, um organizador precisa monitorar a quantidade de pessoas presentes em cada instante. Para cada 2 000 pessoas se faz necessária a presença de um policial. Além disso, estima-se uma densidade de quatro pessoas por metro quadrado de área de terreno ocupado. Às 10 h da manhã, o organizador verifica que a área de terreno já ocupada equivale a um quadrado com lados medindo 500 m. Porém, nas horas seguintes, espera-se que o público aumente a uma taxa de 120 000 pessoas por hora até o início do evento, quando não será mais permitida a entrada de público. Quantos policiais serão necessários no início do evento para garantir a segurança?
a) 360
b) 485
c) 560
d) 740
e) 860
Resolução
Às 10 horas da manhã havia 4 ⋅ 5002 = 1 000 000 de pessoas presentes e até as 4 horas da tarde chegarão mais 120 000 ⋅ 6 = 720 000 pessoas. Portanto, serão necessários 1720 000 / 2000= 860 policiais
Resposta E
Prova Matemática Enem 2016 comentada
QUESTÃO 157 – Enem 2016 prova azul
A permanência de um gerente em uma empresa está condicionada à sua produção no semestre. Essa produção é avaliada pela média do lucro mensal do semestre. Se a média for, no mínimo, de 30 mil reais, o gerente permanece no cargo, caso contrário, ele será despedido. O quadro mostra o lucro mensal, em milhares de reais, dessa empresa, de janeiro a maio do ano em curso. Janeiro Fevereiro Março Abril Maio 21 35 21 30 38 Qual deve ser o lucro mínimo da empresa no mês de junho, em milhares de reais, para o gerente continuar no cargo no próximo semestre?
a) 26
b) 29
c) 30
d) 31
e) 35
Resolução
Sendo x o lucro da empresa no mês de junho, em milhares de reais, temos que:
(21 + 35 + 21 + 30 + 38 + X) / 5 ≥ 30
145 + X ≥ 180
X ≥ 35
Resposta E
Prova Matemática Enem 2016 comentada
QUESTÃO 158 – Enem 2016 prova azul
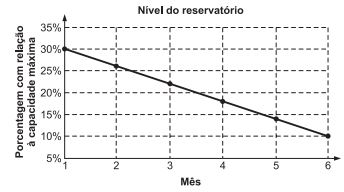
Um dos grandes desafios do Brasil é o gerenciamento dos seus recursos naturais, sobretudo os recursos hídricos. Existe uma demanda crescente por água e o risco de racionamento não pode ser descartado. O nível de água de um reservatório foi monitorado por um período, sendo o resultado mostrado no gráfico. Suponha que essa tendência linear observada no monitoramento se prolongue pelos próximos meses.
 Nas condições dadas, qual o tempo mínimo, após o sexto mês, para que o reservatório atinja o nível zero de sua capacidade?
a) 2 meses e meio.
b) 3 meses e meio.
c) 1 mês e meio.
d) 4 meses.
e) 1 mês.
Resolução
Do gráfico percebemos que ocorre uma variação de (30% – 10%) = 20% no percentual da capacidade máxima do reservatório em 6 – 1 = 5 meses. Assim, para que haja uma redução de 10% do nível de capacidade, deve-se passar
(5 /20)⋅ 10 = 2,5 meses
Resposta A
Nas condições dadas, qual o tempo mínimo, após o sexto mês, para que o reservatório atinja o nível zero de sua capacidade?
a) 2 meses e meio.
b) 3 meses e meio.
c) 1 mês e meio.
d) 4 meses.
e) 1 mês.
Resolução
Do gráfico percebemos que ocorre uma variação de (30% – 10%) = 20% no percentual da capacidade máxima do reservatório em 6 – 1 = 5 meses. Assim, para que haja uma redução de 10% do nível de capacidade, deve-se passar
(5 /20)⋅ 10 = 2,5 meses
Resposta A
Prova Matemática Enem 2016 comentada
QUESTÃO 159 – Enem 2016 prova azul
Um posto de saúde registrou a quantidade de vacinas aplicadas contra febre amarela nos últimos cinco meses:
• 1º mês: 21;
• 2º mês: 22;
• 3º mês: 25;
• 4º mês: 31;
• 5º mês: 21.
No início do primeiro mês, esse posto de saúde tinha 228 vacinas contra febre amarela em estoque. A política de reposição do estoque prevê a aquisição de novas vacinas, no início do sexto mês, de tal forma que a quantidade inicial em estoque para os próximos meses seja igual a 12 vezes a média das quantidades mensais dessas vacinas aplicadas nos últimos cinco meses. Para atender essas condições, a quantidade de vacinas contra febre amarela que o posto de saúde deve adquirir no início do sexto mês é
a) 156.
b) 180.
c) 192.
d) 264.
e) 288.
Resolução
O total de aplicações nos últimos cinco meses foi de 21 + 22 + 25 + 31 + 21 = 120 vacinas, portanto, o posto finalizou o 5º mês com 228 – 120 = 108 vacinas. A quantidade média mensal nesses meses foi de 120/5 = 24 vacinas aplicadas, assim, o estoque inicial do 6º mês deve ser 12 ⋅ 24 = 288, tendo que adquirir 288 – 108 = 180 novas vacinas.
Resposta B
QUESTÃO 160 – Enem 2016 prova azul
Uma liga metálica sai do forno a uma temperatura de 3 000 “C e diminui 1% de sua temperatura a cada 30 min.
Use 0,477 como aproximação para log10(3) e 1,041 como aproximação para log10(11).
O tempo decorrido, em hora, até que a liga atinja 30 °C é mais próximo de
a) 22.
b) 50.
c) 100.
d) 200.
e) 400.
QUESTÃO 152 – Enem 2016 prova azul
Um adolescente vai a um parque de diversões tendo, prioritariamente, o desejo de ir a um brinquedo que se encontra na área IV, dentre as áreas I, II, III, IV e V existentes. O esquema ilustra o mapa do parque, com a localização da entrada, das cinco áreas com os brinquedos disponíveis e dos possíveis caminhos para se chegar a cada área. O adolescente não tem conhecimento do mapa do parque e decide ir caminhando da entrada até chegar à área IV.

Suponha que relativamente a cada ramificação, as opções existentes de percurso pelos caminhos apresentem iguais probabilidades de escolha, que a caminhada foi feita escolhendo ao acaso os caminhos existentes e que, ao tomar um caminho que chegue a uma área distinta da IV, o adolescente necessariamente passa por ela ou retorna. Nessas condições, a probabilidade de ele chegar à área IV sem passar por outras áreas e sem retornar é igual a
a) 1/96
b) 1/64
c) 5/24
d) 1/ 4
e) 5/12
Resolução
Sendo A, B, C, D e E as ramificações como mostradas no desenho anterior, temos apenas dois caminhos sem passar por outras áreas e sem retornar: entrada ” A ” B ” C ” IV e entrada ” A ” D ” E ” IV. Sendo o primeiro com probabilidade 1/2 . 1/2 . 1/3 = 1 /12 e o segundo com probabilidade 1/2 . 1/2 . 1/2 = 1/8
Sendo assim a probabilidade é 1/12 + 1/8 = 5/24
Resposta C
Prova Matemática Enem 2016 comentada
QUESTÃO 153 – Enem 2016 prova azul
Em uma cidade, o número de casos de dengue confirmados aumentou consideravelmente nos últimos dias. A prefeitura resolveu desenvolver uma ação contratando funcionários para ajudar no combate à doença, os quais orientarão os moradores a eliminarem criadouros do mosquito Aedes aegypti, transmissor da dengue. A tabela apresenta o número atual de casos confirmados, por região da cidade.

A prefeitura optou pela seguinte distribuição dos funcionários a serem contratados:
I. 10 funcionários para cada região da cidade cujo número de casos seja maior que a média dos casos confirmados.
II. 7 funcionários para cada região da cidade cujo número de casos seja menor ou igual à média dos casos confirmados.
Quantos funcionários a prefeitura deverá contratar para efetivar a ação?
a) 59
b) 65
c) 68
d) 71
e) 80
Resolução
A média de casos confirmados é dada por
M = (237 + 262 + 158 + 159 + 160 + 278 + 300 + 278) /8 = 229
Das oito regiões da cidade, cinco delas (oeste, centro, leste, centro-oeste e centro-sul) estão acima da média, isto é, cada uma delas receberá 10 funcionários; três regiões estão abaixo da média (norte, sul e noroeste) e cada uma delas receberá 7 funcionários. Portanto, a prefeitura deverá contratar 5 ⋅ 10 + 3 ⋅ 7 = 71 funcionários.
Resposta D
Prova Matemática Enem 2016 comentada
QUESTÃO 154- Enem 2016 prova azul
Cinco marcas de pão integral apresentam as seguintes concentrações de fibras (massa de fibra por massa de pão):
• Marca A: 2 g de fibras a cada 50 g de pão;
• Marca B: 5 g de fibras a cada 40 g de pão;
• Marca C: 5 g de fibras a cada 100 g de pão;
• Marca D: 6 g de fibras a cada 90 g de pão;
• Marca E: 7 g de fibras a cada 70 g de pão.
Recomenda-se a ingestão do pão que possui a maior concentração de fibras. Disponível em: www.blog.saude.gov.br. Acesso em: 25 fev. 2013. A marca a ser escolhida é
a) A.
b) B.
c) C.
d) D.
e) E.
Resolução
Deverá ser escolhida a marca de pão que apresenta a maior razão entre a massa de fibra e a massa de pão. Sendo A, B, C, D e E as razões respectivas de cada marca de pão:
• A = 2/ 50 = 0 040
• B = 5/40 = 0125
• C = 5/100 = 0 050
• D 6/ 90 = 0 066
• E 7/70 = 0100
Como A < C < D < E < B, a marca de pão que escolhida é a B
Resposta B
Prova Matemática Enem 2016 comentada
QUESTÃO 155- Enem 2016 prova azul
Os alunos de uma escola utilizaram cadeiras iguais às da figura para uma aula ao ar livre. A professora, ao final da aula, solicitou que os alunos fechassem as cadeiras para guardá-las. Depois de guardadas, os alunos fizeram um esboço da vista lateral da cadeira fechada.

Resolução
A melhor representação lateral é da letra C
Resposta C
QUESTÃO 156- Enem 2016 prova azul
Para garantir a segurança de um grande evento público que terá início às 4 h da tarde, um organizador precisa monitorar a quantidade de pessoas presentes em cada instante. Para cada 2 000 pessoas se faz necessária a presença de um policial. Além disso, estima-se uma densidade de quatro pessoas por metro quadrado de área de terreno ocupado. Às 10 h da manhã, o organizador verifica que a área de terreno já ocupada equivale a um quadrado com lados medindo 500 m. Porém, nas horas seguintes, espera-se que o público aumente a uma taxa de 120 000 pessoas por hora até o início do evento, quando não será mais permitida a entrada de público. Quantos policiais serão necessários no início do evento para garantir a segurança?
a) 360
b) 485
c) 560
d) 740
e) 860
Resolução
Às 10 horas da manhã havia 4 ⋅ 5002 = 1 000 000 de pessoas presentes e até as 4 horas da tarde chegarão mais 120 000 ⋅ 6 = 720 000 pessoas. Portanto, serão necessários 1720 000 / 2000= 860 policiais
Resposta E
Prova Matemática Enem 2016 comentada
QUESTÃO 157 – Enem 2016 prova azul
A permanência de um gerente em uma empresa está condicionada à sua produção no semestre. Essa produção é avaliada pela média do lucro mensal do semestre. Se a média for, no mínimo, de 30 mil reais, o gerente permanece no cargo, caso contrário, ele será despedido. O quadro mostra o lucro mensal, em milhares de reais, dessa empresa, de janeiro a maio do ano em curso. Janeiro Fevereiro Março Abril Maio 21 35 21 30 38 Qual deve ser o lucro mínimo da empresa no mês de junho, em milhares de reais, para o gerente continuar no cargo no próximo semestre?
a) 26
b) 29
c) 30
d) 31
e) 35
Resolução
Sendo x o lucro da empresa no mês de junho, em milhares de reais, temos que:
(21 + 35 + 21 + 30 + 38 + X) / 5 ≥ 30
145 + X ≥ 180
X ≥ 35
Resposta E
Prova Matemática Enem 2016 comentada
QUESTÃO 158 – Enem 2016 prova azul
Um dos grandes desafios do Brasil é o gerenciamento dos seus recursos naturais, sobretudo os recursos hídricos. Existe uma demanda crescente por água e o risco de racionamento não pode ser descartado. O nível de água de um reservatório foi monitorado por um período, sendo o resultado mostrado no gráfico. Suponha que essa tendência linear observada no monitoramento se prolongue pelos próximos meses.

Nas condições dadas, qual o tempo mínimo, após o sexto mês, para que o reservatório atinja o nível zero de sua capacidade?
a) 2 meses e meio.
b) 3 meses e meio.
c) 1 mês e meio.
d) 4 meses.
e) 1 mês.
Resolução
Do gráfico percebemos que ocorre uma variação de (30% – 10%) = 20% no percentual da capacidade máxima do reservatório em 6 – 1 = 5 meses. Assim, para que haja uma redução de 10% do nível de capacidade, deve-se passar
(5 /20)⋅ 10 = 2,5 meses
Resposta A
Prova Matemática Enem 2016 comentada
QUESTÃO 159 – Enem 2016 prova azul
Um posto de saúde registrou a quantidade de vacinas aplicadas contra febre amarela nos últimos cinco meses:
• 1º mês: 21;
• 2º mês: 22;
• 3º mês: 25;
• 4º mês: 31;
• 5º mês: 21.
No início do primeiro mês, esse posto de saúde tinha 228 vacinas contra febre amarela em estoque. A política de reposição do estoque prevê a aquisição de novas vacinas, no início do sexto mês, de tal forma que a quantidade inicial em estoque para os próximos meses seja igual a 12 vezes a média das quantidades mensais dessas vacinas aplicadas nos últimos cinco meses. Para atender essas condições, a quantidade de vacinas contra febre amarela que o posto de saúde deve adquirir no início do sexto mês é
a) 156.
b) 180.
c) 192.
d) 264.
e) 288.
Resolução
O total de aplicações nos últimos cinco meses foi de 21 + 22 + 25 + 31 + 21 = 120 vacinas, portanto, o posto finalizou o 5º mês com 228 – 120 = 108 vacinas. A quantidade média mensal nesses meses foi de 120/5 = 24 vacinas aplicadas, assim, o estoque inicial do 6º mês deve ser 12 ⋅ 24 = 288, tendo que adquirir 288 – 108 = 180 novas vacinas.
Resposta B
QUESTÃO 160 – Enem 2016 prova azul
Uma liga metálica sai do forno a uma temperatura de 3 000 “C e diminui 1% de sua temperatura a cada 30 min.
Use 0,477 como aproximação para log10(3) e 1,041 como aproximação para log10(11).
O tempo decorrido, em hora, até que a liga atinja 30 °C é mais próximo de
a) 22.
b) 50.
c) 100.
d) 200.
e) 400.
Resolução
Seja x a quantidade decorrida de intervalos de 30 minutos.
A temperatura, em função de x, é:
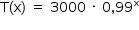 Para T = 30 °C, tem-se:
Para T = 30 °C, tem-se:
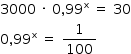 Aplicando-se logaritmo de base 10 em ambos os lados, tem-se:
Aplicando-se logaritmo de base 10 em ambos os lados, tem-se:
 Assim, são necessários 400 · 30 = 12000 minutos, ou seja, 200 horas para que a liga atinja a temperatura de 30 °C.
Assim, são necessários 400 · 30 = 12000 minutos, ou seja, 200 horas para que a liga atinja a temperatura de 30 °C.
Prova Matemática Enem 2016 comentada
Resposta D
QUESTÃO 161 – Enem 2016 prova azul
Um petroleiro possui reservatório em formato de um paralelepípedo retangular com as dimensões dadas por 60 m × 10 m de base e 10 m de altura. Com o objetivo de minimizar o impacto ambiental de um eventual vazamento, esse reservatório é subdividido em três compartimentos, A, B e C, de mesmo volume, por duas placas de aço retangulares com dimensões de 7 m de altura e 10 m de base, de modo que os compartimentos são interligados, conforme a figura. Assim, caso haja rompimento no casco do reservatório, apenas uma parte de sua carga vazará. Suponha que ocorra um desastre quando o petroleiro se encontra com sua carga máxima: ele sofre um acidente que ocasiona um furo no fundo do compartimento C. Para fins de cálculo, considere desprezíveis as espessuras das placas divisórias. Após o fim do vazamento, o volume de petróleo derramado terá sido de
a) 1,4 × 103 m3
b) 1,8 × 103 m3
c) 2,0 × 103 m3
d) 3,2 × 103 m3
e) 6,0 × 103 m3
Resolução
Supondo que o petroleiro fique na posição horizontal, o volume total de petróleo derramado é igual à soma de dois paralelepípedos reto-retângulos: o do compartimento C, de dimensões 60/3 = 20 m, 10 m e 7 m, e o da parte interligada do petroleiro, de dimensões 60 m, 10 m e 10 – 7 = 3 m. Logo, o volume derramado é de
20 ⋅ 10 ⋅ 7 + 60 ⋅ 10 ⋅ 3 = 3,2 ⋅ 103 m3
Resposta D
Prova Matemática Enem 2016 comentada
Seja x a quantidade decorrida de intervalos de 30 minutos.
A temperatura, em função de x, é:
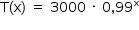
Para T = 30 °C, tem-se:
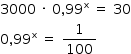
Aplicando-se logaritmo de base 10 em ambos os lados, tem-se:

Assim, são necessários 400 · 30 = 12000 minutos, ou seja, 200 horas para que a liga atinja a temperatura de 30 °C.
Prova Matemática Enem 2016 comentada
Resposta D
QUESTÃO 161 – Enem 2016 prova azul
Um petroleiro possui reservatório em formato de um paralelepípedo retangular com as dimensões dadas por 60 m × 10 m de base e 10 m de altura. Com o objetivo de minimizar o impacto ambiental de um eventual vazamento, esse reservatório é subdividido em três compartimentos, A, B e C, de mesmo volume, por duas placas de aço retangulares com dimensões de 7 m de altura e 10 m de base, de modo que os compartimentos são interligados, conforme a figura. Assim, caso haja rompimento no casco do reservatório, apenas uma parte de sua carga vazará. Suponha que ocorra um desastre quando o petroleiro se encontra com sua carga máxima: ele sofre um acidente que ocasiona um furo no fundo do compartimento C. Para fins de cálculo, considere desprezíveis as espessuras das placas divisórias. Após o fim do vazamento, o volume de petróleo derramado terá sido de
a) 1,4 × 103 m3
b) 1,8 × 103 m3
c) 2,0 × 103 m3
d) 3,2 × 103 m3
e) 6,0 × 103 m3
Resolução
Supondo que o petroleiro fique na posição horizontal, o volume total de petróleo derramado é igual à soma de dois paralelepípedos reto-retângulos: o do compartimento C, de dimensões 60/3 = 20 m, 10 m e 7 m, e o da parte interligada do petroleiro, de dimensões 60 m, 10 m e 10 – 7 = 3 m. Logo, o volume derramado é de
20 ⋅ 10 ⋅ 7 + 60 ⋅ 10 ⋅ 3 = 3,2 ⋅ 103 m3
Resposta D
Prova Matemática Enem 2016 comentada
Questão 162
O cultivo de uma flor rara só é viável se do mês do plantio para o mês subsequente o clima da região possuir as seguintes peculiaridades:
• a variação do nível de chuvas (pluviosidade), nesses meses, não for superior a 50 mm;
• a temperatura mínima, nesses meses, for superior a 15 °C;
• ocorrer, nesse período, um leve aumento não superior a 5 °C na temperatura máxima.
Um floricultor, pretendendo investir no plantio dessa flor em sua região, fez uma consulta a um meteorologista que lhe apresentou o gráfico com as condições previstas para os 12 meses seguintes nessa região.
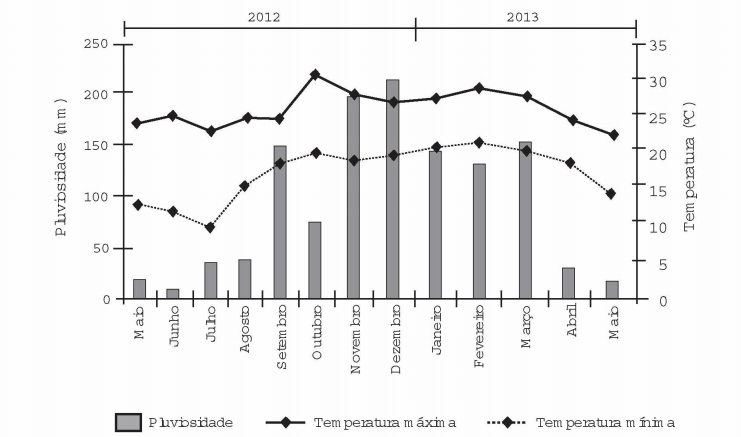 Com base nas informações do gráfico, o floricultor verificou que poderia plantar essa flor rara.
O mês escolhido para o plantio foi
a) janeiro.
b) fevereiro.
c) agosto.
d) novembro.
e) dezembro.
Com base nas informações do gráfico, o floricultor verificou que poderia plantar essa flor rara.
O mês escolhido para o plantio foi
a) janeiro.
b) fevereiro.
c) agosto.
d) novembro.
e) dezembro.
O cultivo de uma flor rara só é viável se do mês do plantio para o mês subsequente o clima da região possuir as seguintes peculiaridades:
• a variação do nível de chuvas (pluviosidade), nesses meses, não for superior a 50 mm;
• a temperatura mínima, nesses meses, for superior a 15 °C;
• ocorrer, nesse período, um leve aumento não superior a 5 °C na temperatura máxima.
Um floricultor, pretendendo investir no plantio dessa flor em sua região, fez uma consulta a um meteorologista que lhe apresentou o gráfico com as condições previstas para os 12 meses seguintes nessa região.

Com base nas informações do gráfico, o floricultor verificou que poderia plantar essa flor rara.
O mês escolhido para o plantio foi
a) janeiro.
b) fevereiro.
c) agosto.
d) novembro.
e) dezembro.
Resolução
Analisando as alternativas dadas, a única que preenche todos os requisitos é a alternativa A (janeiro), uma vez que a variação de pluviosidade de janeiro para fevereiro foi menor que 50 mm; a temperatura mínima naquele mês foi por volta de 20 °C, sendo, portanto, maior que 15 °C. E, de janeiro para fevereiro, houve um leve aumento da temperatura máxima, o qual não excedeu 5 °C, como pedido no enunciado.
Resposta A
Prova Matemática Enem 2016 comentada
QUESTÃO 163 – Enem 2016 prova azul
Densidade absoluta (d) é a razão entre a massa de um corpo e o volume por ele ocupado. Um professor propôs à sua turma que os alunos analisassem a densidade de três corpos: dA, dB, dC. Os alunos verificaram que o corpo A possuía 1,5 vez a massa do corpo B e esse, por sua vez, tinha 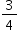 da massa do corpo C. Observaram, ainda, que o volume do corpo A era o mesmo do corpo B e 20% maior do que o volume do corpo C.
Após a análise, os alunos ordenaram corretamente as densidades desses corpos da seguinte maneira
a) dB < dA < dC
b) dB = dA < dC
c) dC < dB = dA
d) dB < dC < dA
e) dC < dB < dA
Resolução
Sejam mx, Vx e dx a massa, o volume e a densidade de x, respectivamente.
Do enunciado:
da massa do corpo C. Observaram, ainda, que o volume do corpo A era o mesmo do corpo B e 20% maior do que o volume do corpo C.
Após a análise, os alunos ordenaram corretamente as densidades desses corpos da seguinte maneira
a) dB < dA < dC
b) dB = dA < dC
c) dC < dB = dA
d) dB < dC < dA
e) dC < dB < dA
Resolução
Sejam mx, Vx e dx a massa, o volume e a densidade de x, respectivamente.
Do enunciado:
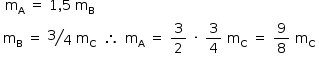 Além disso:
Além disso:
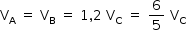 Com isso, tem-se que:
Com isso, tem-se que:
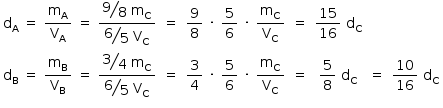 Assim,
Assim, 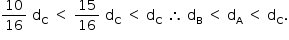 Resposta A
Resposta A
Prova Matemática Enem 2016 comentada
QUESTÃO 164 – Enem 2016 prova azul
No tanque de um certo carro de passeio cabem até 50 L de combustível, e o rendimento médio deste carro na estrada é de 15 km/L de combustível. Ao sair para uma viagem de 600 km o motorista observou que o marcador de combustível estava exatamente sobre uma das marcas da escala divisória do medidor, conforme figura a seguir.
 Como o motorista conhece o percurso, sabe que existem, até a chegada a seu destino, cinco postos de abastecimento de combustível, localizados a 150 km, 187 km, 450 km, 500 km e 570 km do ponto de partida.
Qual a máxima distância, em quilômetro, que poderá percorrer até ser necessário reabastecer o veículo, de modo a não ficar sem combustível na estrada?
a)570
b) 500
c) 450
d) 187
e) 150
Resolução
Com o tanque cheio, o automóvel pode percorrer 50 L · 15 km/L = 750 km.
Observe que a figura do medidor indica que o tanque está com 3/4 da capacidade total. Dessa forma, o automóvel é capaz de percorrer 3/4 · 750 km = 562,5 km sem precisar reabastecer. Porém, para completar a viagem, será necessária uma parada no posto a 500 km do ponto inicial da viagem.
Resposta B
Como o motorista conhece o percurso, sabe que existem, até a chegada a seu destino, cinco postos de abastecimento de combustível, localizados a 150 km, 187 km, 450 km, 500 km e 570 km do ponto de partida.
Qual a máxima distância, em quilômetro, que poderá percorrer até ser necessário reabastecer o veículo, de modo a não ficar sem combustível na estrada?
a)570
b) 500
c) 450
d) 187
e) 150
Resolução
Com o tanque cheio, o automóvel pode percorrer 50 L · 15 km/L = 750 km.
Observe que a figura do medidor indica que o tanque está com 3/4 da capacidade total. Dessa forma, o automóvel é capaz de percorrer 3/4 · 750 km = 562,5 km sem precisar reabastecer. Porém, para completar a viagem, será necessária uma parada no posto a 500 km do ponto inicial da viagem.
Resposta B
Prova Matemática Enem 2016 comentada
QUESTÃO 165 – Enem 2016 prova azul
Sob a orientação de um mestre de obras, João e Pedro trabalharam na reforma de um edifício. João efetuou reparos na parte hidráulica nos andares 1, 3, 5, 7, e assim sucessivamente, de dois em dois andares. Pedro trabalhou na parte elétrica nos andares 1, 4, 7, 10, e assim sucessivamente, de três em três andares. Coincidentemente, terminaram seus trabalhos no último andar. Na conclusão da reforma, o mestre de obras informou, em seu relatório, o número de andares do edifício. Sabe-se que, ao longo da execução da obra, em exatamente 20 andares, foram realizados reparos nas partes hidráulica e elétrica por João e Pedro.
Qual é o número de andares desse edifício?
a) 40
b) 60
c) 100
d) 115
e) 120
Resolução
Do enunciado, depreende-se que os andares em que João e Pedro fazem manutenção representam progressões aritméticas de razões 2 e 3, respectivamente.
João = (1, 3, 5, 7, 9, 11, 13, …)
Pedro = (1, 4, 7, 10, 13, 16, …)
Observe, agora, que os 20 encontros entre eles ocorrem de 6 em 6 andares, formando uma nova progressão aritmética.
Encontros = (1, 7, 13, 19, …)
Aplicando-se a equação do termo geral da P.A., o número de andares será dado por:
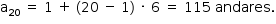 Resposta D
Resposta D
Prova Matemática Enem 2016 comentada
QUESTÃO 166 – Enem 2016 prova azul
Em uma cidade será construída uma galeria subterrânea que receberá uma rede de canos para o transporte de água de uma fonte (F) até o reservatório de um novo bairro (B).
Após avaliações, foram apresentados dois projetos para o trajeto de construção da galeria: um segmento de reta que atravessaria outros bairros ou uma semicircunferência que contornaria esses bairros, conforme ilustrado no sistema de coordenadas xOy da figura, em que a unidade de medida nos eixos é o quilômetro.
 Estudos de viabilidade técnica mostraram que, pelas características do solo, a construção de 1 m de galeria via segmento de reta demora 1,0 h, enquanto que 1 m de construção de galeria via semicircunferência demora 0,6 h. Há urgência em disponibilizar água para esse bairro.
Use 3 como aproximação para π e 1,4 como aproximação para
Estudos de viabilidade técnica mostraram que, pelas características do solo, a construção de 1 m de galeria via segmento de reta demora 1,0 h, enquanto que 1 m de construção de galeria via semicircunferência demora 0,6 h. Há urgência em disponibilizar água para esse bairro.
Use 3 como aproximação para π e 1,4 como aproximação para 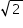 .
O menor tempo possível, em hora, para conclusão da construção da galeria, para atender às necessidades de água do bairro, é de
a) 1 260.
b) 2 520.
c) 2 800.
d) 3 600.
e) 4 000.
Resolução
Projeto “Segmento de Reta”:
A distância entre os pontos B e F é dada por
.
O menor tempo possível, em hora, para conclusão da construção da galeria, para atender às necessidades de água do bairro, é de
a) 1 260.
b) 2 520.
c) 2 800.
d) 3 600.
e) 4 000.
Resolução
Projeto “Segmento de Reta”:
A distância entre os pontos B e F é dada por 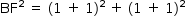
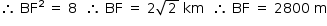 Como o tempo de construção para cada 1 m é de 1 hora, o tempo para execução do projeto é de 2800 horas.
Projeto “Semicircunferência”:
Como o tempo de construção para cada 1 m é de 1 hora, o tempo para execução do projeto é de 2800 horas.
Projeto “Semicircunferência”:
 O comprimento da semicircunferência de raio R é π · R. Mas, segundo a figura,
O comprimento da semicircunferência de raio R é π · R. Mas, segundo a figura,
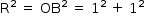 , então
, então 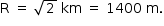 Com isso, o comprimento da galeria é 3 · 1400 m, ou seja, 4200 m.
Como o tempo de construção para cada 1 m é de 0,6 hora, o tempo por hora para execução do projeto é 4200 · 0,6, ou seja, 2520 horas.
Portanto, o menor tempo possível em horas para conclusão da construção da galeria é de 2520 horas.
Resposta B
QUESTÃO 167 – Enem 2016 prova azul
Um túnel deve ser lacrado com uma tampa de concreto. A seção transversal do túnel e a tampa de concreto têm contornos de um arco de parábola e mesmas dimensões. Para determinar o custo da obra, um engenheiro deve calcular a área sob o arco parabólico em questão. Usando o eixo horizontal no nível do chão e o eixo de simetria da parábola como eixo vertical, obteve a seguinte equação para a parábola:
y = 9 – x2, sendo x e y medidos em metros.
Sabe-se que a área sob uma parábola como esta é igual a
Com isso, o comprimento da galeria é 3 · 1400 m, ou seja, 4200 m.
Como o tempo de construção para cada 1 m é de 0,6 hora, o tempo por hora para execução do projeto é 4200 · 0,6, ou seja, 2520 horas.
Portanto, o menor tempo possível em horas para conclusão da construção da galeria é de 2520 horas.
Resposta B
QUESTÃO 167 – Enem 2016 prova azul
Um túnel deve ser lacrado com uma tampa de concreto. A seção transversal do túnel e a tampa de concreto têm contornos de um arco de parábola e mesmas dimensões. Para determinar o custo da obra, um engenheiro deve calcular a área sob o arco parabólico em questão. Usando o eixo horizontal no nível do chão e o eixo de simetria da parábola como eixo vertical, obteve a seguinte equação para a parábola:
y = 9 – x2, sendo x e y medidos em metros.
Sabe-se que a área sob uma parábola como esta é igual a 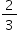 da área do retângulo cujas dimensões são, respectivamente, iguais à base e à altura da entrada do túnel. Qual é a área da parte frontal da tampa de concreto, em metro quadrado?
a) 18
b) 20
c) 36
d) 45
e) 54
da área do retângulo cujas dimensões são, respectivamente, iguais à base e à altura da entrada do túnel. Qual é a área da parte frontal da tampa de concreto, em metro quadrado?
a) 18
b) 20
c) 36
d) 45
e) 54
Analisando as alternativas dadas, a única que preenche todos os requisitos é a alternativa A (janeiro), uma vez que a variação de pluviosidade de janeiro para fevereiro foi menor que 50 mm; a temperatura mínima naquele mês foi por volta de 20 °C, sendo, portanto, maior que 15 °C. E, de janeiro para fevereiro, houve um leve aumento da temperatura máxima, o qual não excedeu 5 °C, como pedido no enunciado.
Resposta A
Prova Matemática Enem 2016 comentada
QUESTÃO 163 – Enem 2016 prova azul
Densidade absoluta (d) é a razão entre a massa de um corpo e o volume por ele ocupado. Um professor propôs à sua turma que os alunos analisassem a densidade de três corpos: dA, dB, dC. Os alunos verificaram que o corpo A possuía 1,5 vez a massa do corpo B e esse, por sua vez, tinha 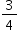 da massa do corpo C. Observaram, ainda, que o volume do corpo A era o mesmo do corpo B e 20% maior do que o volume do corpo C.
da massa do corpo C. Observaram, ainda, que o volume do corpo A era o mesmo do corpo B e 20% maior do que o volume do corpo C.
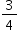 da massa do corpo C. Observaram, ainda, que o volume do corpo A era o mesmo do corpo B e 20% maior do que o volume do corpo C.
da massa do corpo C. Observaram, ainda, que o volume do corpo A era o mesmo do corpo B e 20% maior do que o volume do corpo C.
Após a análise, os alunos ordenaram corretamente as densidades desses corpos da seguinte maneira
a) dB < dA < dC
b) dB = dA < dC
c) dC < dB = dA
d) dB < dC < dA
e) dC < dB < dA
Resolução
Sejam mx, Vx e dx a massa, o volume e a densidade de x, respectivamente.
Do enunciado:
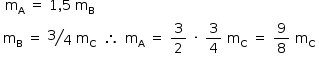
Além disso:
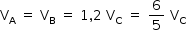
Com isso, tem-se que:
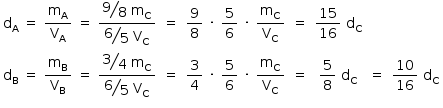
Assim, 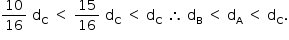
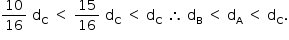
Resposta A
Prova Matemática Enem 2016 comentada
QUESTÃO 164 – Enem 2016 prova azul
No tanque de um certo carro de passeio cabem até 50 L de combustível, e o rendimento médio deste carro na estrada é de 15 km/L de combustível. Ao sair para uma viagem de 600 km o motorista observou que o marcador de combustível estava exatamente sobre uma das marcas da escala divisória do medidor, conforme figura a seguir.

Como o motorista conhece o percurso, sabe que existem, até a chegada a seu destino, cinco postos de abastecimento de combustível, localizados a 150 km, 187 km, 450 km, 500 km e 570 km do ponto de partida.
Qual a máxima distância, em quilômetro, que poderá percorrer até ser necessário reabastecer o veículo, de modo a não ficar sem combustível na estrada?
a)570
b) 500
c) 450
d) 187
e) 150
Resolução
Com o tanque cheio, o automóvel pode percorrer 50 L · 15 km/L = 750 km.
Observe que a figura do medidor indica que o tanque está com 3/4 da capacidade total. Dessa forma, o automóvel é capaz de percorrer 3/4 · 750 km = 562,5 km sem precisar reabastecer. Porém, para completar a viagem, será necessária uma parada no posto a 500 km do ponto inicial da viagem.
Resposta B
Prova Matemática Enem 2016 comentada
QUESTÃO 165 – Enem 2016 prova azul
Sob a orientação de um mestre de obras, João e Pedro trabalharam na reforma de um edifício. João efetuou reparos na parte hidráulica nos andares 1, 3, 5, 7, e assim sucessivamente, de dois em dois andares. Pedro trabalhou na parte elétrica nos andares 1, 4, 7, 10, e assim sucessivamente, de três em três andares. Coincidentemente, terminaram seus trabalhos no último andar. Na conclusão da reforma, o mestre de obras informou, em seu relatório, o número de andares do edifício. Sabe-se que, ao longo da execução da obra, em exatamente 20 andares, foram realizados reparos nas partes hidráulica e elétrica por João e Pedro.
Qual é o número de andares desse edifício?
a) 40
b) 60
c) 100
d) 115
e) 120
Resolução
Do enunciado, depreende-se que os andares em que João e Pedro fazem manutenção representam progressões aritméticas de razões 2 e 3, respectivamente.
João = (1, 3, 5, 7, 9, 11, 13, …)
Pedro = (1, 4, 7, 10, 13, 16, …)
Observe, agora, que os 20 encontros entre eles ocorrem de 6 em 6 andares, formando uma nova progressão aritmética.
Encontros = (1, 7, 13, 19, …)
Aplicando-se a equação do termo geral da P.A., o número de andares será dado por:
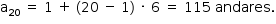
Resposta D
Prova Matemática Enem 2016 comentada
QUESTÃO 166 – Enem 2016 prova azul
Em uma cidade será construída uma galeria subterrânea que receberá uma rede de canos para o transporte de água de uma fonte (F) até o reservatório de um novo bairro (B).
Após avaliações, foram apresentados dois projetos para o trajeto de construção da galeria: um segmento de reta que atravessaria outros bairros ou uma semicircunferência que contornaria esses bairros, conforme ilustrado no sistema de coordenadas xOy da figura, em que a unidade de medida nos eixos é o quilômetro.

Estudos de viabilidade técnica mostraram que, pelas características do solo, a construção de 1 m de galeria via segmento de reta demora 1,0 h, enquanto que 1 m de construção de galeria via semicircunferência demora 0,6 h. Há urgência em disponibilizar água para esse bairro.
Use 3 como aproximação para π e 1,4 como aproximação para 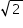 .
.
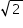 .
.
O menor tempo possível, em hora, para conclusão da construção da galeria, para atender às necessidades de água do bairro, é de
a) 1 260.
b) 2 520.
c) 2 800.
d) 3 600.
e) 4 000.
Resolução
Projeto “Segmento de Reta”:
A distância entre os pontos B e F é dada por 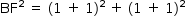
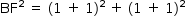
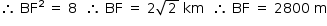
Como o tempo de construção para cada 1 m é de 1 hora, o tempo para execução do projeto é de 2800 horas.
Projeto “Semicircunferência”:

O comprimento da semicircunferência de raio R é π · R. Mas, segundo a figura,
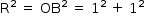 , então
, então 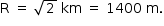
Com isso, o comprimento da galeria é 3 · 1400 m, ou seja, 4200 m.
Como o tempo de construção para cada 1 m é de 0,6 hora, o tempo por hora para execução do projeto é 4200 · 0,6, ou seja, 2520 horas.
Portanto, o menor tempo possível em horas para conclusão da construção da galeria é de 2520 horas.
Resposta B
QUESTÃO 167 – Enem 2016 prova azul
Um túnel deve ser lacrado com uma tampa de concreto. A seção transversal do túnel e a tampa de concreto têm contornos de um arco de parábola e mesmas dimensões. Para determinar o custo da obra, um engenheiro deve calcular a área sob o arco parabólico em questão. Usando o eixo horizontal no nível do chão e o eixo de simetria da parábola como eixo vertical, obteve a seguinte equação para a parábola:
y = 9 – x2, sendo x e y medidos em metros.
Sabe-se que a área sob uma parábola como esta é igual a 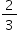 da área do retângulo cujas dimensões são, respectivamente, iguais à base e à altura da entrada do túnel. Qual é a área da parte frontal da tampa de concreto, em metro quadrado?
da área do retângulo cujas dimensões são, respectivamente, iguais à base e à altura da entrada do túnel. Qual é a área da parte frontal da tampa de concreto, em metro quadrado?
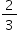 da área do retângulo cujas dimensões são, respectivamente, iguais à base e à altura da entrada do túnel. Qual é a área da parte frontal da tampa de concreto, em metro quadrado?
da área do retângulo cujas dimensões são, respectivamente, iguais à base e à altura da entrada do túnel. Qual é a área da parte frontal da tampa de concreto, em metro quadrado?
a) 18
b) 20
c) 36
d) 45
e) 54
Resolução
Esboçando-se o gráfico de 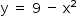 , tem-se:
, tem-se:
- eixo x:
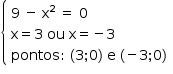
- eixo y:
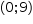
Assim:

- base da entrada do túnel, em metros: 3 + 3 = 6
- altura, em metros: 9
Desse modo, a área A da parte frontal da tampa de concreto, em metros quadrados, é:
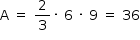
Prova Matemática Enem 2016 comentada
Resposta C
Esboçando-se o gráfico de 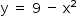 , tem-se:
, tem-se:
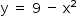 , tem-se:
, tem-se:- eixo x:
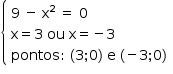
- eixo y:
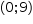
Assim:

- base da entrada do túnel, em metros: 3 + 3 = 6
- altura, em metros: 9
Desse modo, a área A da parte frontal da tampa de concreto, em metros quadrados, é:
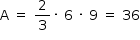
Prova Matemática Enem 2016 comentada
Resposta C
Questão 168
Para cadastrar-se em um site, uma pessoa precisa escolher uma senha composta por quatro caracteres, sendo dois algarismos e duas letras (maiúsculas ou minúsculas). As letras e os algarismos podem estar em qualquer posição. Essa pessoa sabe que o alfabeto é composto por vinte e seis letras e que uma letra maiúscula difere da minúscula em uma senha.
Disponível em: www.infowester.com. Acesso em: 14 dez. 2012.
O número total de senhas possíveis para o cadastramento nesse site é dado por
a) 102 • 262
b) 102 • 522
c) 102 • 522 • 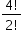 d) 102 • 262 •
d) 102 • 262 • 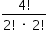 e) 102 • 522 •
e) 102 • 522 • 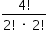
Para cadastrar-se em um site, uma pessoa precisa escolher uma senha composta por quatro caracteres, sendo dois algarismos e duas letras (maiúsculas ou minúsculas). As letras e os algarismos podem estar em qualquer posição. Essa pessoa sabe que o alfabeto é composto por vinte e seis letras e que uma letra maiúscula difere da minúscula em uma senha.
Disponível em: www.infowester.com. Acesso em: 14 dez. 2012.
O número total de senhas possíveis para o cadastramento nesse site é dado por
a) 102 • 262
b) 102 • 522
c) 102 • 522 • 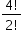
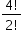
d) 102 • 262 • 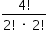
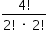
e) 102 • 522 • 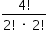
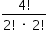
Resolução
Temos algumas informações importantes para resolver esse problema:
- A senha terá 4 caracteres
- sendo dois algarismos e duas letras
- As letras e os algarismos podem estar em qualquer posição.
- O alfabeto tem vinte e seis letras e que uma letra maiúscula difere da minúscula
- São 10 algarismos
- 26 letras maiúsculas + 26 letras minúsculas = 52 letras
Sendo A = algarismo e L = letra, temos : A A L L
Eles poderão permutar pois as letras e os algarismos podem estar em qualquer posição: 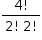 Então o número total de senhas é: 10 . 10. 52. 52 .
Então o número total de senhas é: 10 . 10. 52. 52 . 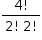 Resposta E
Resposta E
Prova Matemática Enem 2016 comentada
Temos algumas informações importantes para resolver esse problema:
- A senha terá 4 caracteres
- sendo dois algarismos e duas letras
- As letras e os algarismos podem estar em qualquer posição.
- O alfabeto tem vinte e seis letras e que uma letra maiúscula difere da minúscula
- São 10 algarismos
- 26 letras maiúsculas + 26 letras minúsculas = 52 letras
Sendo A = algarismo e L = letra, temos : A A L L
Eles poderão permutar pois as letras e os algarismos podem estar em qualquer posição: 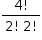
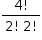
Então o número total de senhas é: 10 . 10. 52. 52 . 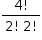
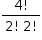
Resposta E
Prova Matemática Enem 2016 comentada
Questão 169
A distribuição de salários pagos em uma empresa pode ser analisada destacando-se a parcela do total da massa salarial que é paga aos 10% que recebem os maiores salários. Isso pode ser representado na forma de um gráfico formado por dois segmentos de reta, unidos em um ponto P, cuja abscissa tem valor igual a 90, como ilustrado na figura.
No eixo horizontal do gráfico tem-se o percentual de funcionários, ordenados de forma crescente pelos valores de seus salários, e no eixo vertical tem-se o percentual do total da massa salarial de todos os funcionários.
 O índice de Gini, que mede o grau de concentração de renda de um determinado grupo, pode ser calculado pela razão
O índice de Gini, que mede o grau de concentração de renda de um determinado grupo, pode ser calculado pela razão 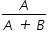 , em que A e B são as medidas das áreas indicadas no gráfico.
A empresa tem como meta tornar seu índice de Gini igual ao do país, que é 0,3. Para tanto, precisa ajustar os salários de modo a alterar o percentual que representa a parcela recebida pelos 10% dos funcionários de maior salário em relação ao total da massa salarial.
Disponível em: www.ipea.gov.br. Acesso em: 4 maio 2016 (adaptado).
Para atingir a meta desejada, o percentual deve ser
a) 40%
b) 20%
c) 60%
d) 30%
e) 70%
, em que A e B são as medidas das áreas indicadas no gráfico.
A empresa tem como meta tornar seu índice de Gini igual ao do país, que é 0,3. Para tanto, precisa ajustar os salários de modo a alterar o percentual que representa a parcela recebida pelos 10% dos funcionários de maior salário em relação ao total da massa salarial.
Disponível em: www.ipea.gov.br. Acesso em: 4 maio 2016 (adaptado).
Para atingir a meta desejada, o percentual deve ser
a) 40%
b) 20%
c) 60%
d) 30%
e) 70%
A distribuição de salários pagos em uma empresa pode ser analisada destacando-se a parcela do total da massa salarial que é paga aos 10% que recebem os maiores salários. Isso pode ser representado na forma de um gráfico formado por dois segmentos de reta, unidos em um ponto P, cuja abscissa tem valor igual a 90, como ilustrado na figura.
No eixo horizontal do gráfico tem-se o percentual de funcionários, ordenados de forma crescente pelos valores de seus salários, e no eixo vertical tem-se o percentual do total da massa salarial de todos os funcionários.

O índice de Gini, que mede o grau de concentração de renda de um determinado grupo, pode ser calculado pela razão 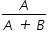 , em que A e B são as medidas das áreas indicadas no gráfico.
, em que A e B são as medidas das áreas indicadas no gráfico.
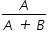 , em que A e B são as medidas das áreas indicadas no gráfico.
, em que A e B são as medidas das áreas indicadas no gráfico.
A empresa tem como meta tornar seu índice de Gini igual ao do país, que é 0,3. Para tanto, precisa ajustar os salários de modo a alterar o percentual que representa a parcela recebida pelos 10% dos funcionários de maior salário em relação ao total da massa salarial.
Disponível em: www.ipea.gov.br. Acesso em: 4 maio 2016 (adaptado).
Para atingir a meta desejada, o percentual deve ser
a) 40%
b) 20%
c) 60%
d) 30%
e) 70%
Resolução
Da figura, tem-se que 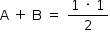 , portanto
, portanto 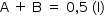 .
Sendo o índice de Gini, como meta, igual a 0,3, tem-se que
.
Sendo o índice de Gini, como meta, igual a 0,3, tem-se que 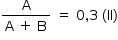 .
Resolvendo-se o sistema dado por (I) e (II), encontra-se A = 0,15 e B = 0,35.
Sendo h a medida do segmento de extremos no ponto P e no ponto (90, 0), a área de B é a soma das áreas de um triângulo e de um trapézio. Assim:
.
Resolvendo-se o sistema dado por (I) e (II), encontra-se A = 0,15 e B = 0,35.
Sendo h a medida do segmento de extremos no ponto P e no ponto (90, 0), a área de B é a soma das áreas de um triângulo e de um trapézio. Assim:
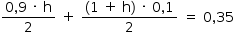 Resolvendo-se a equação, encontra-se:
Resolvendo-se a equação, encontra-se:
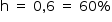 Esses 60% dizem respeito à massa salarial acumulada pelos funcionários que recebem os menores salários, assim, a parcela recebida pelos funcionários de maior salário é 40%.
Resposta A
Esses 60% dizem respeito à massa salarial acumulada pelos funcionários que recebem os menores salários, assim, a parcela recebida pelos funcionários de maior salário é 40%.
Resposta A
Prova Matemática Enem 2016 comentada
Da figura, tem-se que 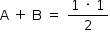 , portanto
, portanto 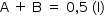 .
.
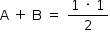 , portanto
, portanto 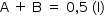 .
.
Sendo o índice de Gini, como meta, igual a 0,3, tem-se que 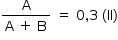 .
.
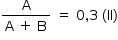 .
.
Resolvendo-se o sistema dado por (I) e (II), encontra-se A = 0,15 e B = 0,35.
Sendo h a medida do segmento de extremos no ponto P e no ponto (90, 0), a área de B é a soma das áreas de um triângulo e de um trapézio. Assim:
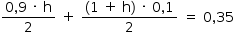
Resolvendo-se a equação, encontra-se:
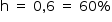
Esses 60% dizem respeito à massa salarial acumulada pelos funcionários que recebem os menores salários, assim, a parcela recebida pelos funcionários de maior salário é 40%.
Resposta A
Prova Matemática Enem 2016 comentada
Questão 170
Ao iniciar suas atividades, um ascensorista registra tanto o número de pessoas que entram quanto o número de pessoas que saem do elevador em cada um dos andares do edifício onde ele trabalha. O quadro apresenta os registros do ascensorista durante a primeira subida do térreo, de onde partem ele e mais três pessoas, ao quinto andar do edifício.
 Com base no quadro, qual é a moda do número de pessoas no elevador durante a subida do térreo ao quinto andar?
a) 2
b) 3
c) 4
d) 5
e) 6
Com base no quadro, qual é a moda do número de pessoas no elevador durante a subida do térreo ao quinto andar?
a) 2
b) 3
c) 4
d) 5
e) 6
Ao iniciar suas atividades, um ascensorista registra tanto o número de pessoas que entram quanto o número de pessoas que saem do elevador em cada um dos andares do edifício onde ele trabalha. O quadro apresenta os registros do ascensorista durante a primeira subida do térreo, de onde partem ele e mais três pessoas, ao quinto andar do edifício.

Com base no quadro, qual é a moda do número de pessoas no elevador durante a subida do térreo ao quinto andar?
a) 2
b) 3
c) 4
d) 5
e) 6
Resolução
Considerando-se, para o cálculo da moda, somente o número de pessoas que entram e saem dos respectivos andares apresentados na tabela, pode-se reescrevê-la da seguinte maneira:
Nº de pessoas
Térreo
1º andar
2º andar
3º andar
4º andar
5º andar
entram
+ 4
+ 4
+ 1
+ 2
+ 2
+ 2
saem
– 0
– 3
– 1
– 2
– 0
– 6
durante a subida
4 – 0 = 4
4 + 4 – 3 = 5
5 + 1 – 1 = 5
5 + 2 – 2 = 5
5 + 2 – 0 = 7
7 + 2 – 6 = 3
Portanto, durante a subida a moda é 5.
Resposta D
Prova Matemática Enem 2016 comentada
Considerando-se, para o cálculo da moda, somente o número de pessoas que entram e saem dos respectivos andares apresentados na tabela, pode-se reescrevê-la da seguinte maneira:
N
|
Térreo
|
1
|
2
|
3
|
4
|
5
|
entram
|
+ 4
|
+ 4
|
+ 1
|
+ 2
|
+ 2
|
+ 2
|
saem
|
– 0
|
– 3
|
– 1
|
– 2
|
– 0
|
– 6
|
durante a subida
|
4 – 0 = 4
|
4 + 4 – 3 = 5
|
5 + 1 – 1 = 5
|
5 + 2 – 2 = 5
|
5 + 2 – 0 = 7
|
7 + 2 – 6 = 3
|
Portanto, durante a subida a moda é 5.
Resposta D
Prova Matemática Enem 2016 comentada
Questão 171
O censo demográfico é um levantamento estatístico que permite a coleta de várias informações. A tabela apresenta os dados obtidos pelo censo demográfico brasileiro nos anos de 1940 e 2000, referentes à concentração da população total, na capital e no interior, nas cinco grandes regiões.
População residente, na capital e interior segundo as Grandes Regiões 1940/2000
 Fonte: IBGE, Censo Demográfico 1940/2000.
O valor mais próximo do percentual que descreve o aumento da população nas capitais da Região Nordeste é
a) 125%
b) 231%
c) 331%
d) 700%
e) 800%
Resolução
A população nas capitais da região Nordeste foi, segundo o gráfico, de 1 270 729 em 1940 para 10 162 346 em 2000. Então, o percentual que descreve o aumento pedido é:
Fonte: IBGE, Censo Demográfico 1940/2000.
O valor mais próximo do percentual que descreve o aumento da população nas capitais da Região Nordeste é
a) 125%
b) 231%
c) 331%
d) 700%
e) 800%
Resolução
A população nas capitais da região Nordeste foi, segundo o gráfico, de 1 270 729 em 1940 para 10 162 346 em 2000. Então, o percentual que descreve o aumento pedido é:
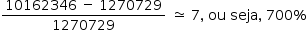 Resposta D
Resposta D
Prova Matemática Enem 2016 comentada
O censo demográfico é um levantamento estatístico que permite a coleta de várias informações. A tabela apresenta os dados obtidos pelo censo demográfico brasileiro nos anos de 1940 e 2000, referentes à concentração da população total, na capital e no interior, nas cinco grandes regiões.
População residente, na capital e interior segundo as Grandes Regiões 1940/2000

Fonte: IBGE, Censo Demográfico 1940/2000.
O valor mais próximo do percentual que descreve o aumento da população nas capitais da Região Nordeste é
a) 125%
b) 231%
c) 331%
d) 700%
e) 800%
Resolução
A população nas capitais da região Nordeste foi, segundo o gráfico, de 1 270 729 em 1940 para 10 162 346 em 2000. Então, o percentual que descreve o aumento pedido é:
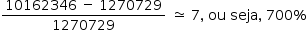
Resposta D
Prova Matemática Enem 2016 comentada
Questão 172
Um marceneiro está construindo um material didático que corresponde ao encaixe de peças de madeira com 10 cm de altura e formas geométricas variadas, num bloco de madeira em que cada peça se posicione na perfuração com seu formato correspondente, conforme ilustra a figura. O bloco de madeira já possui três perfurações prontas de bases distintas: uma quadrada (Q), de lado 4 cm, uma retangular (R), com base 3 cm e altura 4 cm, e uma em forma de um triângulo equilátero (T), de lado 6,8 cm. Falta realizar uma perfuração de base circular (C).
O marceneiro não quer que as outras peças caibam na perfuração circular e nem que a peça de base circular caiba nas demais perfurações e, para isso, escolherá o diâmetro do círculo que atenda a tais condições. Procurou em suas ferramentas uma serra copo (broca com formato circular) para perfurar a base em madeira, encontrando cinco exemplares, com diferentes medidas de diâmetros, como segue: (l) 3,8 cm; (II) 4,7 cm; (III) 5,6 cm; (IV) 7,2 cm e (V) 9,4 cm.
 Considere 1,4 e 1,7 como aproximações para
Considere 1,4 e 1,7 como aproximações para 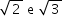 , respectivamente.
Para que seja atingido o seu objetivo, qual dos exemplares de serra copo o marceneiro deverá escolher?
a) I
b) II
c) III
d) IV
e) V
Resolução
Uma análise sobre possíveis valores para o diâmetro do círculo pode ser feita comparando-o com alguns elementos dos quadriláteros.
Sejam DQ e DR as diagonais do quadrado e do retângulo, respectivamente, e R o raio do círculo, tem-se:
, respectivamente.
Para que seja atingido o seu objetivo, qual dos exemplares de serra copo o marceneiro deverá escolher?
a) I
b) II
c) III
d) IV
e) V
Resolução
Uma análise sobre possíveis valores para o diâmetro do círculo pode ser feita comparando-o com alguns elementos dos quadriláteros.
Sejam DQ e DR as diagonais do quadrado e do retângulo, respectivamente, e R o raio do círculo, tem-se:
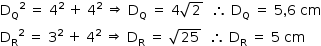 (I) Quadrado e círculo
Observe as figuras:
(I) Quadrado e círculo
Observe as figuras:
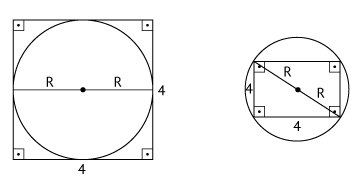 Para que o círculo não caiba no quadrado, seu diâmetro deve ser maior que o lado do quadrado, e, para que o quadrado não caiba no círculo, o diâmetro do círculo precisa ser menor do que a diagonal do quadrado. Então:
Para que o círculo não caiba no quadrado, seu diâmetro deve ser maior que o lado do quadrado, e, para que o quadrado não caiba no círculo, o diâmetro do círculo precisa ser menor do que a diagonal do quadrado. Então:
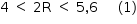 (II) Retângulo e círculo
Observe as figuras:
(II) Retângulo e círculo
Observe as figuras:
 Para que o círculo não caiba no retângulo, seu diâmetro deve ser maior do que a menor dimensão do retângulo, e, para que o retângulo não caiba no círculo, o diâmetro do círculo precisa ser menor do que a diagonal do retângulo. Então:
Para que o círculo não caiba no retângulo, seu diâmetro deve ser maior do que a menor dimensão do retângulo, e, para que o retângulo não caiba no círculo, o diâmetro do círculo precisa ser menor do que a diagonal do retângulo. Então:
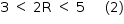 Das condições (1) e (2), tem-se:
Das condições (1) e (2), tem-se:
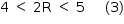 Assim, entre os valores apresentados no texto para o diâmetro do círculo, o único que atinge o objetivo do marceneiro é 4,7 cm.
Resposta B
Assim, entre os valores apresentados no texto para o diâmetro do círculo, o único que atinge o objetivo do marceneiro é 4,7 cm.
Resposta B
Prova Matemática Enem 2016 comentada
Um marceneiro está construindo um material didático que corresponde ao encaixe de peças de madeira com 10 cm de altura e formas geométricas variadas, num bloco de madeira em que cada peça se posicione na perfuração com seu formato correspondente, conforme ilustra a figura. O bloco de madeira já possui três perfurações prontas de bases distintas: uma quadrada (Q), de lado 4 cm, uma retangular (R), com base 3 cm e altura 4 cm, e uma em forma de um triângulo equilátero (T), de lado 6,8 cm. Falta realizar uma perfuração de base circular (C).
O marceneiro não quer que as outras peças caibam na perfuração circular e nem que a peça de base circular caiba nas demais perfurações e, para isso, escolherá o diâmetro do círculo que atenda a tais condições. Procurou em suas ferramentas uma serra copo (broca com formato circular) para perfurar a base em madeira, encontrando cinco exemplares, com diferentes medidas de diâmetros, como segue: (l) 3,8 cm; (II) 4,7 cm; (III) 5,6 cm; (IV) 7,2 cm e (V) 9,4 cm.

Considere 1,4 e 1,7 como aproximações para 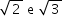 , respectivamente.
, respectivamente.
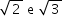 , respectivamente.
, respectivamente.
Para que seja atingido o seu objetivo, qual dos exemplares de serra copo o marceneiro deverá escolher?
a) I
b) II
c) III
d) IV
e) V
Resolução
Uma análise sobre possíveis valores para o diâmetro do círculo pode ser feita comparando-o com alguns elementos dos quadriláteros.
Sejam DQ e DR as diagonais do quadrado e do retângulo, respectivamente, e R o raio do círculo, tem-se:
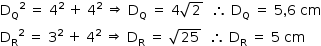
(I) Quadrado e círculo
Observe as figuras:

Para que o círculo não caiba no quadrado, seu diâmetro deve ser maior que o lado do quadrado, e, para que o quadrado não caiba no círculo, o diâmetro do círculo precisa ser menor do que a diagonal do quadrado. Então:
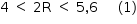
(II) Retângulo e círculo
Observe as figuras:

Para que o círculo não caiba no retângulo, seu diâmetro deve ser maior do que a menor dimensão do retângulo, e, para que o retângulo não caiba no círculo, o diâmetro do círculo precisa ser menor do que a diagonal do retângulo. Então:
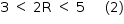
Das condições (1) e (2), tem-se:
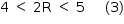
Assim, entre os valores apresentados no texto para o diâmetro do círculo, o único que atinge o objetivo do marceneiro é 4,7 cm.
Resposta B
Prova Matemática Enem 2016 comentada
Questão 173
Em um exame, foi feito o monitoramento dos níveis de duas substâncias presentes (A e B) na corrente sanguínea de uma pessoa, durante um período de 24 h, conforme o resultado apresentado na figura. Um nutricionista, no intuito de prescrever uma dieta para essa pessoa, analisou os níveis dessas substâncias, determinando que, para uma dieta semanal eficaz, deverá ser estabelecido um parâmetro cujo valor será dado pelo número de vezes em que os níveis de A e de B forem iguais, porém, maiores que o nível mínimo da substância A durante o período de duração da dieta.
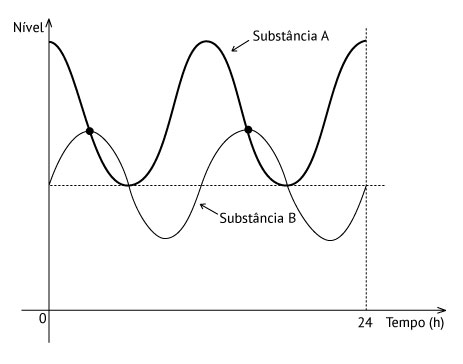 Considere que o padrão apresentado no resultado do exame, no período analisado, se repita para os dias subsequentes.
O valor do parâmetro estabelecido pelo nutricionista, para uma dieta semanal, será igual a
a) 28.
b) 21.
c) 2.
d) 7.
e) 14.
Resolução
Observando-se a figura tem-se, a cada 24 horas, dois pontos comuns aos gráficos que correspondem a níveis maiores que o nível mínimo da substância A.
Considere que o padrão apresentado no resultado do exame, no período analisado, se repita para os dias subsequentes.
O valor do parâmetro estabelecido pelo nutricionista, para uma dieta semanal, será igual a
a) 28.
b) 21.
c) 2.
d) 7.
e) 14.
Resolução
Observando-se a figura tem-se, a cada 24 horas, dois pontos comuns aos gráficos que correspondem a níveis maiores que o nível mínimo da substância A.
 Assim, em uma semana, isso ocorre 14 vezes.
Resposta E
QUESTÃO 174 – Enem 2016 prova azul
Um paciente necessita de reidratação endovenosa feita por meio de cinco frascos de soro durante 24 h. Cada frasco tem um volume de 800 mL de soro. Nas primeiras quatro horas, deverá receber 40% do total a ser aplicado. Cada mililitro de soro corresponde a 12 gotas. O número de gotas por minuto que o paciente deverá receber após as quatro primeiras horas será
a) 16.
b) 20.
c) 24.
d) 34.
e) 40.
Resolução
O volume total de soro é 800 mL ⋅ 5 = 4 000 mL. Nas primeiras 4 horas o paciente receberá 40% do total, nas últimas 20 horas ele receberá 100% – 40% = 60% do total, o que corresponde a 60% ⋅ 4 000 mL = 2 400 mL. Sendo o mililitro de soro = 12 gotas, o número de gotas por minuto é:
(2400.12)/(20.60) = 24 gotas / minuto
Resposta C
Assim, em uma semana, isso ocorre 14 vezes.
Resposta E
QUESTÃO 174 – Enem 2016 prova azul
Um paciente necessita de reidratação endovenosa feita por meio de cinco frascos de soro durante 24 h. Cada frasco tem um volume de 800 mL de soro. Nas primeiras quatro horas, deverá receber 40% do total a ser aplicado. Cada mililitro de soro corresponde a 12 gotas. O número de gotas por minuto que o paciente deverá receber após as quatro primeiras horas será
a) 16.
b) 20.
c) 24.
d) 34.
e) 40.
Resolução
O volume total de soro é 800 mL ⋅ 5 = 4 000 mL. Nas primeiras 4 horas o paciente receberá 40% do total, nas últimas 20 horas ele receberá 100% – 40% = 60% do total, o que corresponde a 60% ⋅ 4 000 mL = 2 400 mL. Sendo o mililitro de soro = 12 gotas, o número de gotas por minuto é:
(2400.12)/(20.60) = 24 gotas / minuto
Resposta C
Prova Matemática Enem 2016 comentada
QUESTÃO 175- Enem 2016 prova azul
É comum os artistas plásticos se apropriarem de entes matemáticos para produzirem, por exemplo, formas e imagens por meio de manipulações. Um artista plástico, em uma de suas obras, pretende retratar os diversos polígonos obtidos pelas intersecções de um plano com uma pirâmide regular de base quadrada. Segundo a classificação dos polígonos, quais deles são possíveis de serem obtidos pelo artista plástico?
a) Quadrados, apenas.
b) Triângulos e quadrados, apenas.
c) Triângulos, quadrados e trapézios, apenas.
d) Triângulos, quadrados, trapézios e quadriláteros irregulares, apenas.
e) Triângulos, quadrados, trapézios, quadriláteros irregulares e pentágonos, apenas.
Resolução
Prova Matemática Enem 2016 comentada
Admitindo que um quadrilátero irregular é um quadrilátero que não é um trapézio, podemos obter, como intersecção entre um plano e uma pirâmide regular de base quadrada, triângulos, quadrados, trapézios, quadriláteros irregulares e pentágonos, conforme os exemplos a seguir:
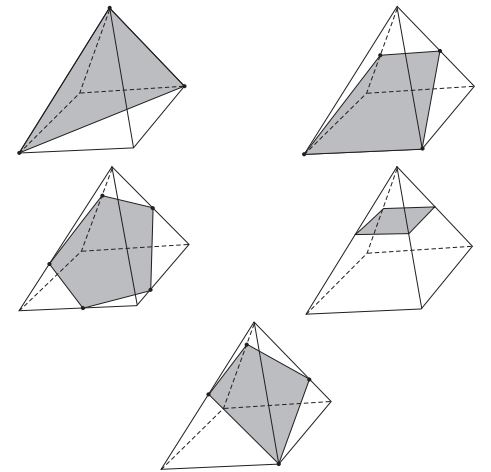 Resposta E
Resposta E
Prova Matemática Enem 2016 comentada
QUESTÃO 176- Enem 2016 prova azul
Um reservatório é abastecido com água por uma torneira e um ralo faz a drenagem da água desse reservatório. Os gráficos representam as vazões Q, em litro por minuto, do volume de água que entra no reservatório pela torneira e do volume que sai pelo ralo, em função do tempo t, em minuto.
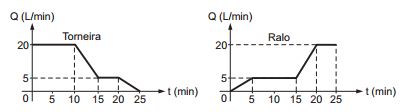 Em qual intervalo de tempo, em minuto, o reservatório tem uma vazão constante de enchimento?
a) De 0 a 10.
b) De 5 a 10.
c) De 5 a 15.
d) De 15 a 25.
e) De 0 a 25.
Resoluções
Sendo Q1(t) e Q2(t) as vazões, em litros por minuto, da torneira e do ralo, respectivamente, a vazão do reservatório é V(t) = Q1(t) – Q2(t). Para que V(t) seja constante, devemos ter, de acordo com o gráfico, duas situações possíveis:
• Q1(t) e Q2(t) são constantes, o que só ocorre no intervalo [5; 10]; ou
• Q1(t) e Q2(t) são funções de primeiro grau com o mesmo coeficiente angular, o que não ocorre em algum intervalo.
Resposta B
Prova Matemática Enem 2016 comentada
QUESTÃO 177- Enem 2016 prova azul
O LIRAa, Levantamento Rápido do Índice de Infestação por Aedes aegypti, consiste num mapeamento da infestação do mosquito Aedes aegypti. O LIRAa é dado pelo percentual do número de imóveis com focos do mosquito, entre os escolhidos de uma região em avaliação.
O serviço de vigilância sanitária de um município, no mês de outubro do ano corrente, analisou o LIRAa de cinco bairros que apresentaram o maior índice de infestação no ano anterior. Os dados obtidos para cada bairro foram:
I. 14 imóveis com focos de mosquito em 400 imóveis no bairro;
II. 6 imóveis com focos de mosquito em 500 imóveis no bairro;
III. 13 imóveis com focos de mosquito em 520 imóveis no bairro;
IV. 9 imóveis com focos de mosquito em 360 imóveis no bairro;
V. 15 imóveis com focos de mosquito em 500 imóveis no bairro.
O setor de dedetização do município definiu que o direcionamento das ações de controle iniciarão pelo bairro que apresentou o maior índice do LIRAa. Disponível em: http://bvsms.saude.gov.br. Acesso em: 28 out. 2015. As ações de controle iniciarão pelo bairro
a) I.
b) II.
c) III.
d) IV.
e) V.
Resoluções
Os índices de LIRAa dos bairros I, II, III, IV e V são, respectivamente:
14/400 = 0,035 =3,5%
6/500 = 0,012 = 1,2%
13/520 = 0,025 = 2,5%
9/360 = 0,025 = 2,5%
15/500 = 0,03 = 3%
Assim, as ações de controle iniciarão pelo bairro I.
Resposta A
QUESTÃO 178- Enem 2016 prova azul
A figura representa o globo terrestre e nela estão marcados os pontos A, B e C. Os pontos A e B estão localizados sobre um mesmo paralelo, e os pontos B e C, sobre um mesmo meridiano. É traçado um caminho do ponto A até C, pela superfície do globo, passando por B, de forma que o trecho de A até B se dê sobre o paralelo que passa por A e B e, o trecho de B até C se dê sobre o meridiano que passa por B e C. Considere que o plano α é paralelo à linha do equador na figura.
Em qual intervalo de tempo, em minuto, o reservatório tem uma vazão constante de enchimento?
a) De 0 a 10.
b) De 5 a 10.
c) De 5 a 15.
d) De 15 a 25.
e) De 0 a 25.
Resoluções
Sendo Q1(t) e Q2(t) as vazões, em litros por minuto, da torneira e do ralo, respectivamente, a vazão do reservatório é V(t) = Q1(t) – Q2(t). Para que V(t) seja constante, devemos ter, de acordo com o gráfico, duas situações possíveis:
• Q1(t) e Q2(t) são constantes, o que só ocorre no intervalo [5; 10]; ou
• Q1(t) e Q2(t) são funções de primeiro grau com o mesmo coeficiente angular, o que não ocorre em algum intervalo.
Resposta B
Prova Matemática Enem 2016 comentada
QUESTÃO 177- Enem 2016 prova azul
O LIRAa, Levantamento Rápido do Índice de Infestação por Aedes aegypti, consiste num mapeamento da infestação do mosquito Aedes aegypti. O LIRAa é dado pelo percentual do número de imóveis com focos do mosquito, entre os escolhidos de uma região em avaliação.
O serviço de vigilância sanitária de um município, no mês de outubro do ano corrente, analisou o LIRAa de cinco bairros que apresentaram o maior índice de infestação no ano anterior. Os dados obtidos para cada bairro foram:
I. 14 imóveis com focos de mosquito em 400 imóveis no bairro;
II. 6 imóveis com focos de mosquito em 500 imóveis no bairro;
III. 13 imóveis com focos de mosquito em 520 imóveis no bairro;
IV. 9 imóveis com focos de mosquito em 360 imóveis no bairro;
V. 15 imóveis com focos de mosquito em 500 imóveis no bairro.
O setor de dedetização do município definiu que o direcionamento das ações de controle iniciarão pelo bairro que apresentou o maior índice do LIRAa. Disponível em: http://bvsms.saude.gov.br. Acesso em: 28 out. 2015. As ações de controle iniciarão pelo bairro
a) I.
b) II.
c) III.
d) IV.
e) V.
Resoluções
Os índices de LIRAa dos bairros I, II, III, IV e V são, respectivamente:
14/400 = 0,035 =3,5%
6/500 = 0,012 = 1,2%
13/520 = 0,025 = 2,5%
9/360 = 0,025 = 2,5%
15/500 = 0,03 = 3%
Assim, as ações de controle iniciarão pelo bairro I.
Resposta A
QUESTÃO 178- Enem 2016 prova azul
A figura representa o globo terrestre e nela estão marcados os pontos A, B e C. Os pontos A e B estão localizados sobre um mesmo paralelo, e os pontos B e C, sobre um mesmo meridiano. É traçado um caminho do ponto A até C, pela superfície do globo, passando por B, de forma que o trecho de A até B se dê sobre o paralelo que passa por A e B e, o trecho de B até C se dê sobre o meridiano que passa por B e C. Considere que o plano α é paralelo à linha do equador na figura.
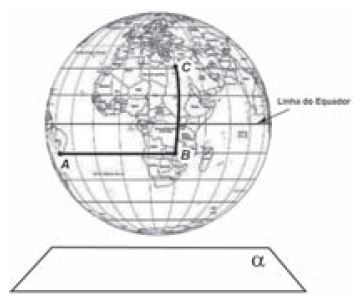 A projeção ortogonal, no plano , do caminho traçado no
globo pode ser representada por
A projeção ortogonal, no plano , do caminho traçado no
globo pode ser representada por
-
a

-
b

-
c

-
d

-
e
 Resolução
Resolução
Sendo A e B pontos sobre o mesmo paralelo, a projeção de A para B será um arco de circunferência paralelo à linha do equador.
 Seja D o ponto da trajetória de B para C que pertence à linha do equador. Assim, pode-se dividir o segundo trajeto em duas partes: de B para D e de D para C.
Seja D o ponto da trajetória de B para C que pertence à linha do equador. Assim, pode-se dividir o segundo trajeto em duas partes: de B para D e de D para C.
 De B para D, a projeção será um segmento radial, no sentido da linha do equador.
De D para C, a projeção será um segmento radial, no sentido do centro.
Resposta E
De B para D, a projeção será um segmento radial, no sentido da linha do equador.
De D para C, a projeção será um segmento radial, no sentido do centro.
Resposta E
QUESTÃO 179 – Enem 2016 prova azul
Diante da hipótese do comprometimento da qualidade da água retirada do volume morto de alguns sistemas hídricos, os técnicos de um laboratório decidiram testar cinco tipos de filtros de água. Dentre esses, os quatro com melhor desempenho serão escolhidos para futura comercialização. Nos testes, foram medidas as massas de agentes contaminantes, em miligrama, que não são capturados por cada filtro em diferentes períodos, em dia, como segue: • Filtro 1 (F1): 18 mg em 6 dias;
Filtro 2 (F2): 15 mg em 3 dias;
Filtro 3 (F3): 18 mg em 4 dias;
Filtro 4 (F4): 6 mg em 3 dias;
Filtro 5 (F5): 3 mg em 2 dias.
Ao final, descarta-se o filtro com a maior razão entre a medida da massa de contaminantes não capturados e o número de dias, o que corresponde ao de pior desempenho.
Disponível em: www.redebrasilatual.com.br. Acesso em: 12 jul. 2015 (adaptado).
O filtro descartado é o
a) F1.
b) F2.
c) F3.
d) F4.
e) F5.
Resolução
As razões entre as medidas das massas de agentes contaminantes não capturados e o número de dias, de cada filtro, estão descritas a seguir:
Filtro 1: 18mg/6 dias = 3,0mg/dia
Filtro 2: 15mg/3 dias = 5,0mg/dia
Filtro 3: 18mg/4 dias = 4,5 mg/dia
Filtro 4: 6mg/3 dias = 2,0mg/dia
Filtro 5: 3mg/2 dias = 1,5 mg/dia
Sendo assim o filtro com maior razão (divisão) será o descartado: 2
Em um exame, foi feito o monitoramento dos níveis de duas substâncias presentes (A e B) na corrente sanguínea de uma pessoa, durante um período de 24 h, conforme o resultado apresentado na figura. Um nutricionista, no intuito de prescrever uma dieta para essa pessoa, analisou os níveis dessas substâncias, determinando que, para uma dieta semanal eficaz, deverá ser estabelecido um parâmetro cujo valor será dado pelo número de vezes em que os níveis de A e de B forem iguais, porém, maiores que o nível mínimo da substância A durante o período de duração da dieta.

Considere que o padrão apresentado no resultado do exame, no período analisado, se repita para os dias subsequentes.
O valor do parâmetro estabelecido pelo nutricionista, para uma dieta semanal, será igual a
a) 28.
b) 21.
c) 2.
d) 7.
e) 14.
Resolução
Observando-se a figura tem-se, a cada 24 horas, dois pontos comuns aos gráficos que correspondem a níveis maiores que o nível mínimo da substância A.

Assim, em uma semana, isso ocorre 14 vezes.
Resposta E
QUESTÃO 174 – Enem 2016 prova azul
Um paciente necessita de reidratação endovenosa feita por meio de cinco frascos de soro durante 24 h. Cada frasco tem um volume de 800 mL de soro. Nas primeiras quatro horas, deverá receber 40% do total a ser aplicado. Cada mililitro de soro corresponde a 12 gotas. O número de gotas por minuto que o paciente deverá receber após as quatro primeiras horas será
a) 16.
b) 20.
c) 24.
d) 34.
e) 40.
Resolução
O volume total de soro é 800 mL ⋅ 5 = 4 000 mL. Nas primeiras 4 horas o paciente receberá 40% do total, nas últimas 20 horas ele receberá 100% – 40% = 60% do total, o que corresponde a 60% ⋅ 4 000 mL = 2 400 mL. Sendo o mililitro de soro = 12 gotas, o número de gotas por minuto é:
(2400.12)/(20.60) = 24 gotas / minuto
Resposta C
Prova Matemática Enem 2016 comentada
QUESTÃO 175- Enem 2016 prova azul
É comum os artistas plásticos se apropriarem de entes matemáticos para produzirem, por exemplo, formas e imagens por meio de manipulações. Um artista plástico, em uma de suas obras, pretende retratar os diversos polígonos obtidos pelas intersecções de um plano com uma pirâmide regular de base quadrada. Segundo a classificação dos polígonos, quais deles são possíveis de serem obtidos pelo artista plástico?
a) Quadrados, apenas.
b) Triângulos e quadrados, apenas.
c) Triângulos, quadrados e trapézios, apenas.
d) Triângulos, quadrados, trapézios e quadriláteros irregulares, apenas.
e) Triângulos, quadrados, trapézios, quadriláteros irregulares e pentágonos, apenas.
Resolução
Prova Matemática Enem 2016 comentada
Admitindo que um quadrilátero irregular é um quadrilátero que não é um trapézio, podemos obter, como intersecção entre um plano e uma pirâmide regular de base quadrada, triângulos, quadrados, trapézios, quadriláteros irregulares e pentágonos, conforme os exemplos a seguir:

Resposta E
Prova Matemática Enem 2016 comentada
QUESTÃO 176- Enem 2016 prova azul
Um reservatório é abastecido com água por uma torneira e um ralo faz a drenagem da água desse reservatório. Os gráficos representam as vazões Q, em litro por minuto, do volume de água que entra no reservatório pela torneira e do volume que sai pelo ralo, em função do tempo t, em minuto.

Em qual intervalo de tempo, em minuto, o reservatório tem uma vazão constante de enchimento?
a) De 0 a 10.
b) De 5 a 10.
c) De 5 a 15.
d) De 15 a 25.
e) De 0 a 25.
Resoluções
Sendo Q1(t) e Q2(t) as vazões, em litros por minuto, da torneira e do ralo, respectivamente, a vazão do reservatório é V(t) = Q1(t) – Q2(t). Para que V(t) seja constante, devemos ter, de acordo com o gráfico, duas situações possíveis:
• Q1(t) e Q2(t) são constantes, o que só ocorre no intervalo [5; 10]; ou
• Q1(t) e Q2(t) são funções de primeiro grau com o mesmo coeficiente angular, o que não ocorre em algum intervalo.
Resposta B
Prova Matemática Enem 2016 comentada
QUESTÃO 177- Enem 2016 prova azul
O LIRAa, Levantamento Rápido do Índice de Infestação por Aedes aegypti, consiste num mapeamento da infestação do mosquito Aedes aegypti. O LIRAa é dado pelo percentual do número de imóveis com focos do mosquito, entre os escolhidos de uma região em avaliação.
O serviço de vigilância sanitária de um município, no mês de outubro do ano corrente, analisou o LIRAa de cinco bairros que apresentaram o maior índice de infestação no ano anterior. Os dados obtidos para cada bairro foram:
I. 14 imóveis com focos de mosquito em 400 imóveis no bairro;
II. 6 imóveis com focos de mosquito em 500 imóveis no bairro;
III. 13 imóveis com focos de mosquito em 520 imóveis no bairro;
IV. 9 imóveis com focos de mosquito em 360 imóveis no bairro;
V. 15 imóveis com focos de mosquito em 500 imóveis no bairro.
O setor de dedetização do município definiu que o direcionamento das ações de controle iniciarão pelo bairro que apresentou o maior índice do LIRAa. Disponível em: http://bvsms.saude.gov.br. Acesso em: 28 out. 2015. As ações de controle iniciarão pelo bairro
a) I.
b) II.
c) III.
d) IV.
e) V.
Resoluções
Os índices de LIRAa dos bairros I, II, III, IV e V são, respectivamente:
14/400 = 0,035 =3,5%
6/500 = 0,012 = 1,2%
13/520 = 0,025 = 2,5%
9/360 = 0,025 = 2,5%
15/500 = 0,03 = 3%
Assim, as ações de controle iniciarão pelo bairro I.
Resposta A
QUESTÃO 178- Enem 2016 prova azul
A figura representa o globo terrestre e nela estão marcados os pontos A, B e C. Os pontos A e B estão localizados sobre um mesmo paralelo, e os pontos B e C, sobre um mesmo meridiano. É traçado um caminho do ponto A até C, pela superfície do globo, passando por B, de forma que o trecho de A até B se dê sobre o paralelo que passa por A e B e, o trecho de B até C se dê sobre o meridiano que passa por B e C. Considere que o plano α é paralelo à linha do equador na figura.

A projeção ortogonal, no plano , do caminho traçado no
globo pode ser representada por
a

b

c
d
e

Resolução
Sendo A e B pontos sobre o mesmo paralelo, a projeção de A para B será um arco de circunferência paralelo à linha do equador.

Seja D o ponto da trajetória de B para C que pertence à linha do equador. Assim, pode-se dividir o segundo trajeto em duas partes: de B para D e de D para C.

De B para D, a projeção será um segmento radial, no sentido da linha do equador.
De D para C, a projeção será um segmento radial, no sentido do centro.
Resposta E
QUESTÃO 179 – Enem 2016 prova azul
Diante da hipótese do comprometimento da qualidade da água retirada do volume morto de alguns sistemas hídricos, os técnicos de um laboratório decidiram testar cinco tipos de filtros de água. Dentre esses, os quatro com melhor desempenho serão escolhidos para futura comercialização. Nos testes, foram medidas as massas de agentes contaminantes, em miligrama, que não são capturados por cada filtro em diferentes períodos, em dia, como segue: • Filtro 1 (F1): 18 mg em 6 dias;
Filtro 2 (F2): 15 mg em 3 dias;
Filtro 3 (F3): 18 mg em 4 dias;
Filtro 4 (F4): 6 mg em 3 dias;
Filtro 5 (F5): 3 mg em 2 dias.
Ao final, descarta-se o filtro com a maior razão entre a medida da massa de contaminantes não capturados e o número de dias, o que corresponde ao de pior desempenho.
Disponível em: www.redebrasilatual.com.br. Acesso em: 12 jul. 2015 (adaptado).
O filtro descartado é o
a) F1.
b) F2.
c) F3.
d) F4.
e) F5.
Resolução
As razões entre as medidas das massas de agentes contaminantes não capturados e o número de dias, de cada filtro, estão descritas a seguir:
Filtro 1: 18mg/6 dias = 3,0mg/dia
Filtro 2: 15mg/3 dias = 5,0mg/dia
Filtro 3: 18mg/4 dias = 4,5 mg/dia
Filtro 4: 6mg/3 dias = 2,0mg/dia
Filtro 5: 3mg/2 dias = 1,5 mg/dia
Sendo assim o filtro com maior razão (divisão) será o descartado: 2
Prova Matemática Enem 2016 comentada
Resposta B
Resposta B
Prova Matemática Enem 2016 comentada
Questão 180
Em 2011, um terremoto de magnitude 9,0 na escala Richter causou um devastador tsunami no Japão, provocando um alerta na usina nuclear de Fukushima. Em 2013, outro terremoto, de magnitude 7,0 na mesma escala, sacudiu Sichuan (sudoeste da China), deixando centenas de mortos e milhares de feridos. A magnitude de um terremoto na escala Richter pode ser calculada por
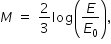 sendo E a energia, em kWh, liberada pelo terremoto e E0 uma constante real positiva. Considere que E1 e E2representam as energias liberadas nos terremotos ocorridos no Japão e na China, respectivamente.
Disponível em: www.terra.com.br. Acesso em: 15 ago. 2013 (adaptado).
Qual a relação entre E1 e E2?
a) E1 = E2 + 2
b) E1 = 102 • E2
c) E1 = 103 • E2
d) E1 =
sendo E a energia, em kWh, liberada pelo terremoto e E0 uma constante real positiva. Considere que E1 e E2representam as energias liberadas nos terremotos ocorridos no Japão e na China, respectivamente.
Disponível em: www.terra.com.br. Acesso em: 15 ago. 2013 (adaptado).
Qual a relação entre E1 e E2?
a) E1 = E2 + 2
b) E1 = 102 • E2
c) E1 = 103 • E2
d) E1 = 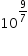 • E2
e) E1 =
• E2
e) E1 = 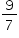 • E2
Resolução
• E2
Resolução
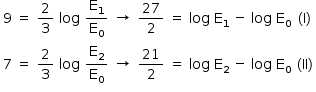 Multiplicando a equação (II) por –1 e somando-se com a equação (I) tem-se:
Multiplicando a equação (II) por –1 e somando-se com a equação (I) tem-se:
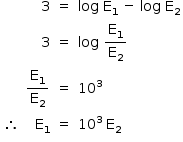 Resposta C
Resposta C
Em 2011, um terremoto de magnitude 9,0 na escala Richter causou um devastador tsunami no Japão, provocando um alerta na usina nuclear de Fukushima. Em 2013, outro terremoto, de magnitude 7,0 na mesma escala, sacudiu Sichuan (sudoeste da China), deixando centenas de mortos e milhares de feridos. A magnitude de um terremoto na escala Richter pode ser calculada por
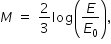
sendo E a energia, em kWh, liberada pelo terremoto e E0 uma constante real positiva. Considere que E1 e E2representam as energias liberadas nos terremotos ocorridos no Japão e na China, respectivamente.
Disponível em: www.terra.com.br. Acesso em: 15 ago. 2013 (adaptado).
Qual a relação entre E1 e E2?
a) E1 = E2 + 2
b) E1 = 102 • E2
c) E1 = 103 • E2
d) E1 = 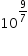 • E2
• E2
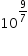 • E2
• E2
e) E1 = 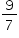 • E2
• E2
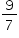 • E2
• E2
Resolução
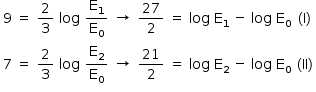
Multiplicando a equação (II) por –1 e somando-se com a equação (I) tem-se:
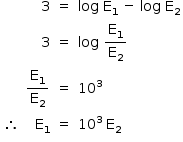
Resposta C
Prova Matemática Enem 2016 comentada - COMPLETA
 Reviewed by Tiago Gomes
on
julho 25, 2017
Rating:
Reviewed by Tiago Gomes
on
julho 25, 2017
Rating:
 Reviewed by Tiago Gomes
on
julho 25, 2017
Rating:
Reviewed by Tiago Gomes
on
julho 25, 2017
Rating:




Nenhum comentário: